Gina subscribes to a cell phone service that charges a monthly fee of $60.00. The first 500 megabytes of data is free, and the cost is $0.15 for each additional megabyte of data used that month. Which of the following functions gives the cost, in dollars, for a month in which Gina uses x megabytes of data, where x>500.
60+15x
0.15x−15
0.15x−440
60+0.15x
The correct Answer is:B
To find the cost function for Gina's cell phone service when she uses more than 500 megabytes (MB) of data, we can break down the problem step by step.
Step 1: Identify the fixed cost
Gina has a monthly fee of $60. This is a fixed cost that she pays regardless of her data usage.
Hint: Remember that fixed costs do not change with the level of service used.
Step 2: Determine the free data allowance
The first 500 MB of data is free. This means that if Gina uses up to 500 MB, she will not incur any additional charges.
Hint: Free allowances can significantly affect the total cost, so always account for them first.
Step 3: Calculate additional data usage
Since Gina uses more than 500 MB, we need to calculate how much additional data she uses. If she uses x MB, the additional data used is given by:
\( \text{Additional Data} = x - 500 \)
Hint: Always subtract the free allowance from the total usage to find the additional cost.
Step 4: Determine the cost of additional data
The cost for each additional MB used beyond the free 500 MB is $0.15. Therefore, the total cost for the additional data is:
\( \text{Cost of Additional Data} = 0.15 \times (x - 500) \)
Hint: Multiplying the additional data by the cost per MB gives the total additional cost.
Step 5: Formulate the total cost function
Now, we can combine the fixed cost and the cost of additional data to get the total cost function:
\(
\text{Total Cost} = \text{Fixed Cost} + \text{Cost of Additional Data}
\)
Substituting the values we have:
\(
\text{Total Cost} = 60 + 0.15(x - 500)
\)
Step 6: Simplify the cost function
Now we simplify the expression:
\(
\text{Total Cost} = 60 + 0.15x - 0.15 \times 500
\)
Calculating \(0.15 \times 500\):
\(
0.15 \times 500 = 75
\)
So, we have:
\(
\text{Total Cost} = 60 + 0.15x - 75
\)
Combining the constant terms:
\(
\text{Total Cost} = 0.15x + (60 - 75) = 0.15x - 15
\)
Final Cost Function
Thus, the cost function for Gina when she uses more than 500 MB is:
\(
\text{Cost} = 0.15x - 15
\)
Conclusion
From the provided options, the correct function that represents the cost in dollars for a month in which Gina uses \(x\) megabytes of data (where \(x > 500\)) is:
Option 2: \(0.15x - 15\).
---
Gina has a monthly fee of $60. This is a fixed cost that she pays regardless of her data usage.
The first 500 MB of data is free. This means that if Gina uses up to 500 MB, she will not incur any additional charges.
Since Gina uses more than 500 MB, we need to calculate how much additional data she uses. If she uses x MB, the additional data used is given by:
\( \text{Additional Data} = x - 500 \)
The cost for each additional MB used beyond the free 500 MB is $0.15. Therefore, the total cost for the additional data is:
\( \text{Cost of Additional Data} = 0.15 \times (x - 500) \)
Now, we can combine the fixed cost and the cost of additional data to get the total cost function:
\(
\text{Total Cost} = \text{Fixed Cost} + \text{Cost of Additional Data}
\)
Substituting the values we have:
\(
\text{Total Cost} = 60 + 0.15(x - 500)
\)
Now we simplify the expression:
\(
\text{Total Cost} = 60 + 0.15x - 0.15 \times 500
\)
Calculating \(0.15 \times 500\):
\(
0.15 \times 500 = 75
\)
So, we have:
\(
\text{Total Cost} = 60 + 0.15x - 75
\)
Combining the constant terms:
\(
\text{Total Cost} = 0.15x + (60 - 75) = 0.15x - 15
\)
Thus, the cost function for Gina when she uses more than 500 MB is:
\(
\text{Cost} = 0.15x - 15
\)
From the provided options, the correct function that represents the cost in dollars for a month in which Gina uses \(x\) megabytes of data (where \(x > 500\)) is:
Option 2: \(0.15x - 15\).
Similar Questions
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load isView SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively areView Solution
Knowledge Check
- Question 1 - Select One
A text messaging plan charges a flat fee of $5 per month for up to 100 text messages sent plus $0.25 for each additional text message sent that month. Which of the following graphs represents the cost, y, of sending x texts in a month?
A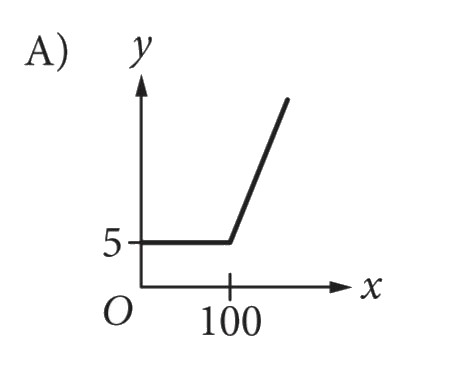 B
B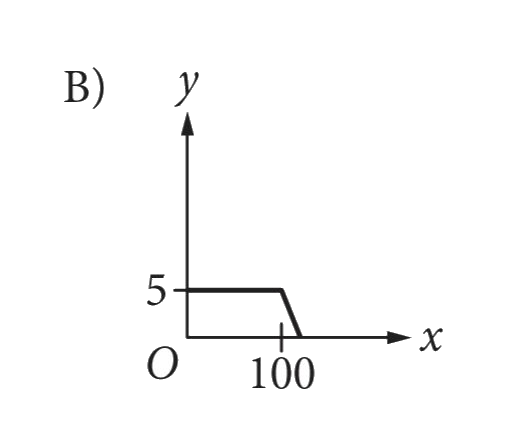 C
C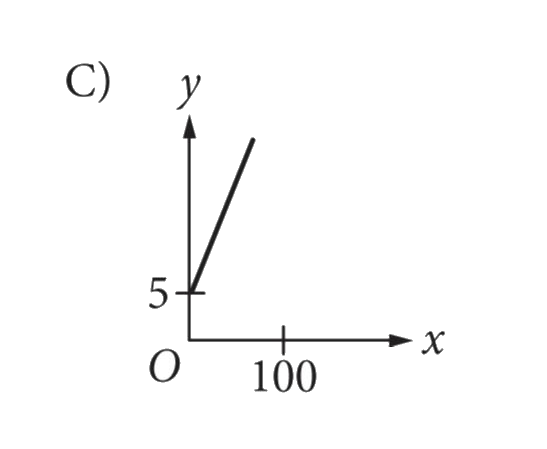 D
D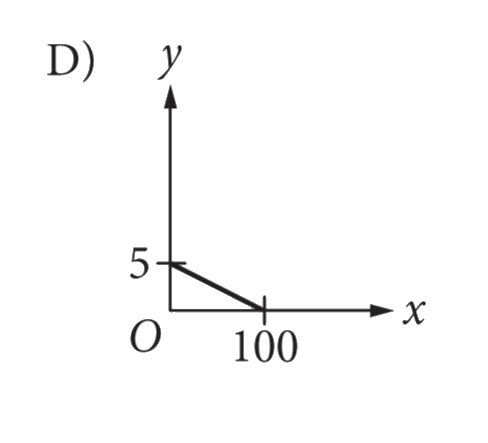
- Question 2 - Select One
C=60+0.25d
The equation represents the monthly cost of a cell phone that includes up to 1 gigabyte of data after which there is a charge for d gigabytes of any additional data. Which of the following must be true?
I. The cost of each additional megabyte of data is $60.25.
II. The y-intercept of the graph of the cost equation represents the charge for each additional megabytes of data used.
III. If betwee 5 and 6 megabytes of data are used in month, the monthly charge is $61.25.AI and II onlyBI and III onlyCII onlyDIII only - Question 3 - Select One
In 2014, the United States Postal Service charged $0.48 to mail a first class letter weighing upto 1oz. And $0.21 for each additional ounce. Based on these rates which function would determine the cost, in dollars, c(z), of meiling a first-class letter weighing z ounces where z is an integer greater than 1?
Ac(z)=0.48z+0.21Bc(z)=0.21z+0.48Cc(z)=0.48(z−1)+0.21Dc(z)=0.21(z−1)+0.48
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1View SolutionTamara has a cell phone that charges $0.07 per minute plus a monthly fee of $19.00. She budgets $29.50 per month for total cell phone expenses without taxes. What is the maximum number of minutes. Tamara could use her phone each month in order to stay withi her budget?
View SolutionA storage facility is currently offering a special rate to customers who sign contracts for 6 months or more. According to this special rate, the first month's rent is $1, and for each month after the first month, customers pay the regular monthly rental rate. The table below shows the storage unit sizes avialble, the floor dimensions, and the regular monthly rental rate. All the units have the same heigher.

Janelle, the owner of the storage facility, is considering building new units that have floor dimensions larger than size 5 units. She will use the floor area to determine the heating requirements of these larger units. For this calculation, Janelle will use the same relationship between the unit size number and the respective floor area for sizes 1 through 5, which of the following expressions gives the floor area, in square meters, of a Size x storage unit?View SolutionC=60+0.05d
The equation above represents the total monthly cost, C, in dollars of a data plan offered by a cell phone company when the data usage in a month exceeds a 1 gigabyte limit by d megabytes. According to the model, what is the meaning of 0.05?View SolutionAdriana used the data from a scatterplot she found on the U.S. Census Bureau's website to determine a regression model showing the relationship between the population in the area where she lived and the number of years, x, after she was born. The result was an exponential growth equation of the form y=x0(1+r)x. Which of the following does x0 most likely represent in the equation ?
View Solution

