
In the figure above, line l is parallel to line k. Transversals m and n intersect at point P on l and intersect k at point R and Q, respectively. Point Y is on k, the measure of ∠PRY is 140∘, and the measures of ∠QPR is 100∘. How many of the angles formed by rays l, k, m, and n have measure 40∘?
4
6
8
10
The correct Answer is:C
Similar Questions
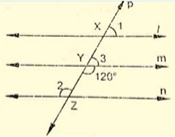
In Fig. l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View Solution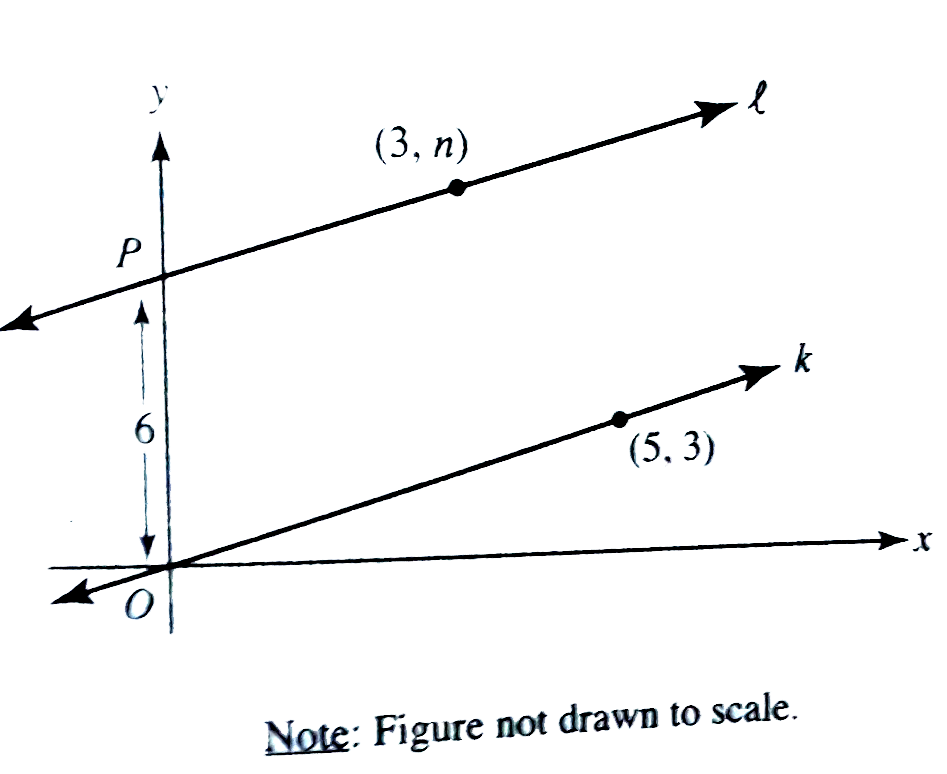
In the xy-coordinate system shown above , the lines l and k are parallel , and distance OP is 6. if the points (5,3) is on line k , and the point (3,n) is on line l. what is the value of n ?
View Solution
Knowledge Check

In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35∘, what is the measure of ∠2 ?A35∘B55∘C70∘D145∘In the figure below, line m is perpendicular to line n, and both lines intersect line q at the same point. The measure of ∠1 is (3x−10)∘, and the measure of ∠2 is (2x+10)∘. What is the measure of ∠3?
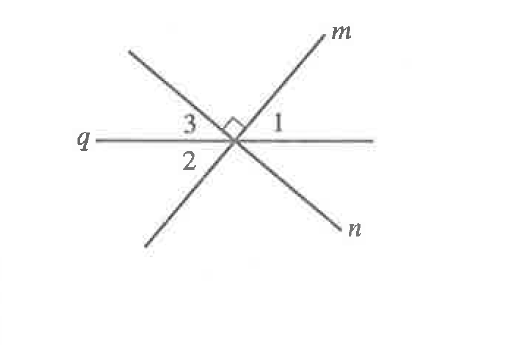 A36∘B40∘C44∘D45∘
A36∘B40∘C44∘D45∘Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
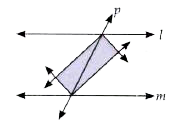 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
In the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
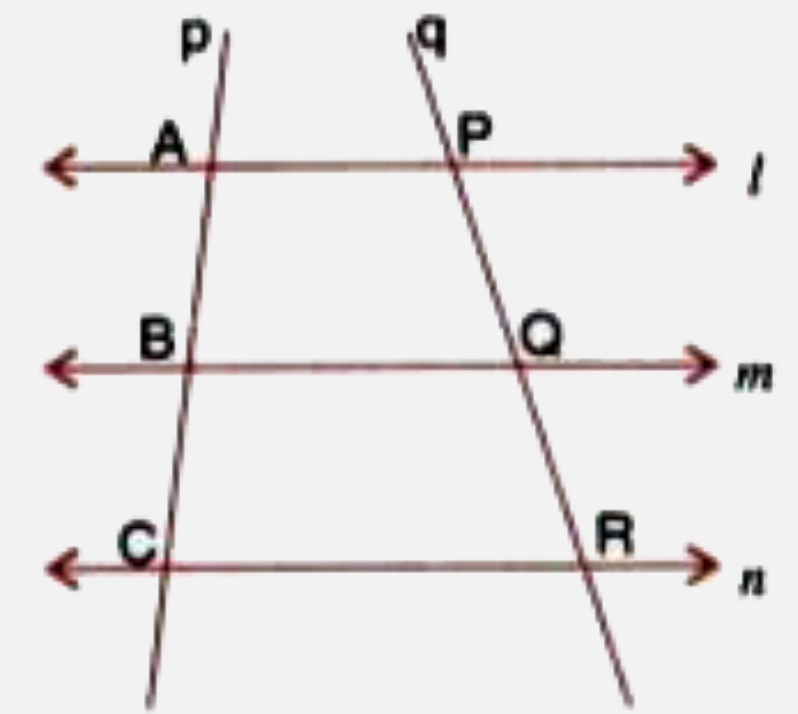
Prove that : ABBC=PQQR
Join A and R. Let AR meets BQ at point D.
View SolutionIn the given figure l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

View SolutionIn Figure, l,mandn are parallel lines intersected by a transversal at X,Y,andZ respectively. Find ∠1, ∠2 and∠3. Give reasons.
Let∠1=3xand∠2=2x
∠1+∠2=180∘
⇒5x=180∘
x=36∘
∠1=108∘,∠2=72∘
Since m∥nand l is the intersector
∠3=∠1=108∘ and ∠4=∠2=72∘ (Opposite angles
∠7=∠5=∠2=72∘
=∠5=72∘
∠6=108∘=∠8
View Solution
