Line k contains the point (4, 0) and has slope 5. Which of the following points is on line k?
(1, 5)
(3, 5)
(5, 5)
(7, 5)
The correct Answer is:C
To solve the problem of finding which point lies on line k, we will follow these steps:
Step 1: Determine the equation of line k
Given that line k contains the point (4, 0) and has a slope of 5, we can use the point-slope form of the equation of a line:
y−y1=m(x−x1)
Where:
- (x1,y1) is the point on the line, which is (4, 0).
- m is the slope, which is 5.
Substituting the values into the equation:
y−0=5(x−4)
This simplifies to:
y=5x−20
Step 2: Check each option to see which point satisfies the equation
We will check each point provided in the options to see if it satisfies the equation y=5x−20.
1. Option A: (1, -15)
- Substitute x=1:
y=5(1)−20=5−20=−15
- This point satisfies the equation.
2. Option B: (3, -5)
- Substitute x=3:
y=5(3)−20=15−20=−5
- This point satisfies the equation.
3. Option C: (5, 5)
- Substitute x=5:
y=5(5)−20=25−20=5
- This point satisfies the equation.
4. Option D: (0, -20)
- Substitute x=0:
y=5(0)−20=0−20=−20
- This point satisfies the equation.
Conclusion
All points satisfy the equation y=5x−20. However, since the question asks for which point is on line k, we can conclude that the point (5, 5) is indeed on line k.
Given that line k contains the point (4, 0) and has a slope of 5, we can use the point-slope form of the equation of a line:
- (x1,y1) is the point on the line, which is (4, 0).
- m is the slope, which is 5.
We will check each point provided in the options to see if it satisfies the equation y=5x−20.
- Substitute x=1:
y=5(1)−20=5−20=−15
- This point satisfies the equation.
- Substitute x=3:
y=5(3)−20=15−20=−5
- This point satisfies the equation.
- Substitute x=5:
y=5(5)−20=25−20=5
- This point satisfies the equation.
- Substitute x=0:
y=5(0)−20=0−20=−20
- This point satisfies the equation.
All points satisfy the equation y=5x−20. However, since the question asks for which point is on line k, we can conclude that the point (5, 5) is indeed on line k.
Similar Questions
Knowledge Check
Line m in the xy-plane contains the points (2, 4) and (0, 1).Which of the following is an equation of line m ?
Ay = 2x + 3By = 2x + 4Cy=32x+3Dy=32x+1A line in the xy-plane passes through the origin and has a slope of 17. Which of the following points lies on the line?
A(0, 7)B(1, 7)C(7, 7)D(14, 2)Line A passes through the cooredinate points (−25,0)and(0,1). Which of the following lines will line A never intersect ?
A B
B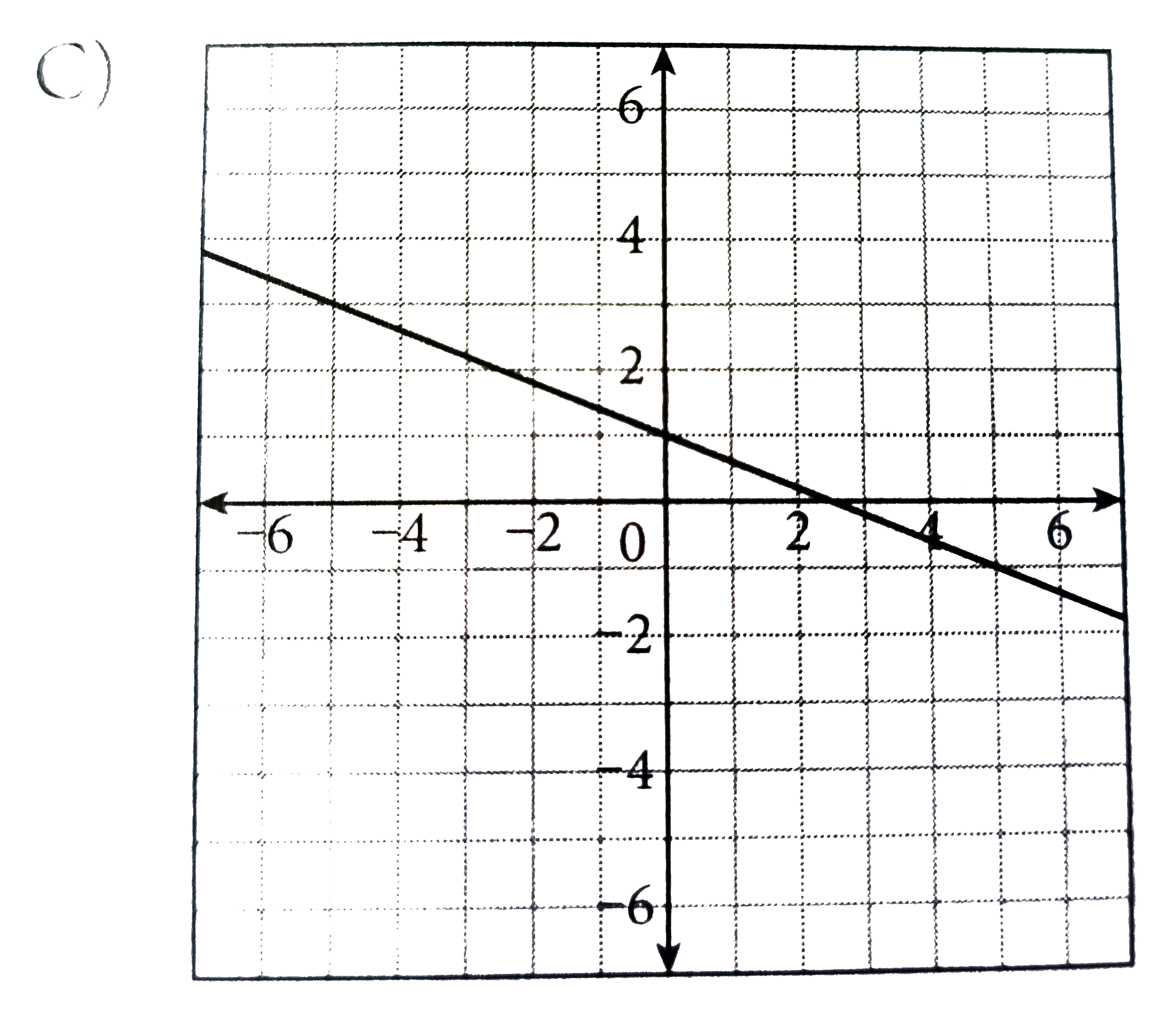 C
C D
D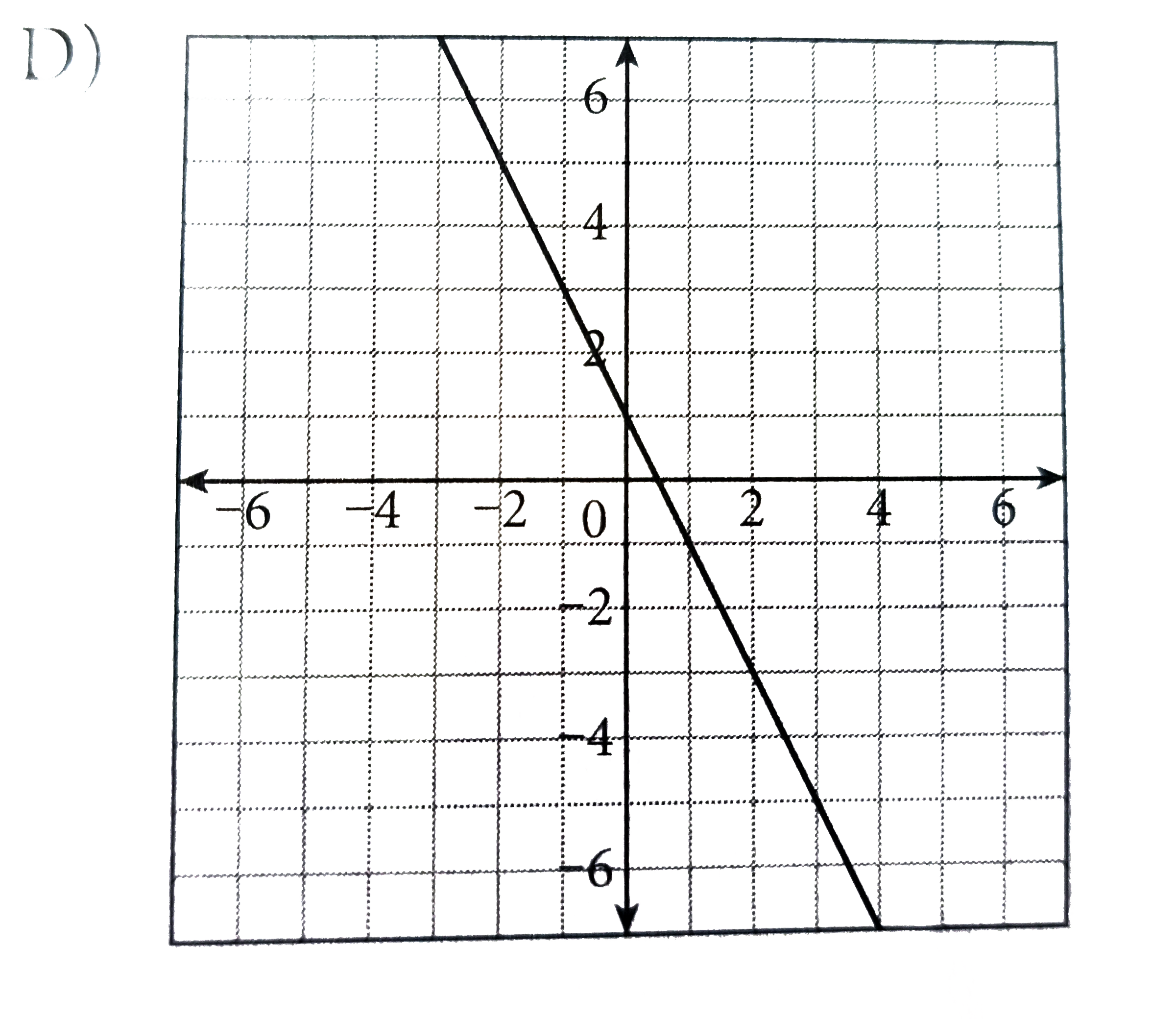
Line f in th exy-plane passes through the origin and has a slope of −25. Line z is perpendicular to line f and passes through the point (6,2). Which of the following is the equation of line z ?
View SolutionThe line y=kx+4 , where k is a constant, is graphed in the xy-plane. If the line contains the point (c, d) where c≠0 and d≠0, what is the slope of the line in terms of c and d ?
View SolutionThe equation of the line containing the point (4,−5) and parallel to the line joining the points (3,7) and (-2,4) is
View Solution6 In the xy-plane, the line determined by the points (2,k) and (32,k) passes through the origin. Which of the following could be the value of k ?
View SolutionLine L has an undefined slope. Line M is perpendicular to line L. Which of the following could be the equation of line M?
View Solution
