A cylinder has volume V, height h, and base diameter d. Which of the following represents d in terms of V and h?
d=√Vπh
d=√vπh
d=√2Vπh
d=√4Vπh
The correct Answer is:D
To find the diameter d of a cylinder in terms of its volume V and height h, we can follow these steps:
Step 1: Write the formula for the volume of a cylinder.
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base of the cylinder and h is the height.
Step 2: Relate the radius to the diameter.
The radius r is half of the diameter d:
r=d2
Step 3: Substitute the expression for r into the volume formula.
Substituting r=d2 into the volume formula, we get:
V=π(d2)2h
Step 4: Simplify the equation.
This simplifies to:
V=π(d24)h
which can be rewritten as:
V=πd2h4
Step 5: Solve for d2.
To isolate d2, we multiply both sides by 4:
4V=πd2h
Now, divide both sides by πh:
d2=4Vπh
Step 6: Take the square root to find d.
Taking the square root of both sides, we find:
d=√4Vπh
Final Result:
Thus, the diameter d in terms of the volume V and height h is:
d=√4Vπh
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base of the cylinder and h is the height.
The radius r is half of the diameter d:
r=d2
Substituting r=d2 into the volume formula, we get:
V=π(d2)2h
This simplifies to:
V=π(d24)h
which can be rewritten as:
V=πd2h4
To isolate d2, we multiply both sides by 4:
4V=πd2h
Now, divide both sides by πh:
d2=4Vπh
Taking the square root of both sides, we find:
d=√4Vπh
Thus, the diameter d in terms of the volume V and height h is:
d=√4Vπh
Similar Questions
A cylinder with radius r and height h is closed on the top and bottom. Which of the following expressions represents the total surface area of this cylinder? (a) 2πr (r+h) (b) πr (r+2h) (c) πr (2r+h) (d) 2πr2+h
View SolutionThe density d of an object is found by dividing the mass m of the object by its volume V. Which of the following equations gives the mass m in terms of d and V?
View Solution
Knowledge Check
- Question 1 - Select One
h=−16t2+vt+k
The equation above gives the height h, in feet, of a ball t seconds after it is thrown straight up with an initial speed of v feet per second from a height of k feet. Which of the following gives v in terms of h, t, and k ?Av=h+k−16tBv=h−k+16tCv=h+kt−16tDv=h−kt+16t - Question 2 - Select One
If V=13Bh, what is h expressed in terms of B and V?
A13BVBV3BC3VBD3VB - Question 3 - Select One
Suppose the evaporation rate of water in a lake is given by the equation E=Ta−Tb700−VTwh4, where E is the evaporation rate in gallons/day. Ta is the air temperature, Td is the dew point temperature, V is the volume of water in the table, Tw is the water temperature, and h is the number of hours the water is exposed to sunlight. Which of the following expresses Tw in terms Ta,Tb,V,E,andh?
ATw=Eh4(Ta−Tb)VBTw=700Ta−Td−Eh4VCTw=V4(Ta−Tb)Eh4DTw=VTa−Td700−Eh4
If g is same at a height h and at a depth d, then
View SolutionD is the distance from vertex F to vertex G. The base is square, and the height is twice the width. What is the volume of the solid in terms of d ?
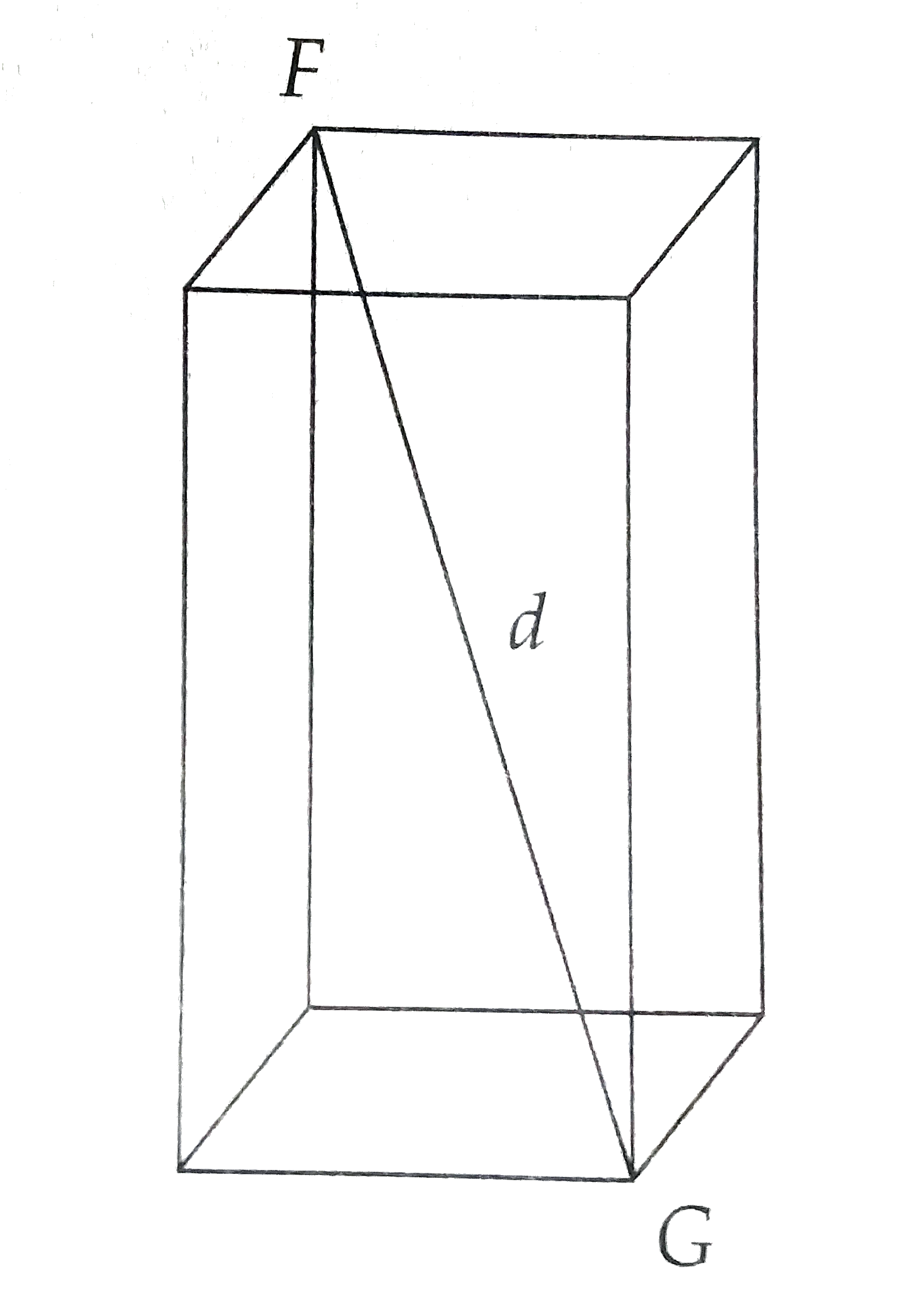 View Solution
View SolutionA cylinder has a surface area of 360π and height of 3. What is the diameter of the cylinder's circular base?
View SolutionV=13π(d2)2h
A circle of rubber with a constant diameter d is placed on a table, its perimeter is anchored to the table and a string is attached to its centre. When the string is pulled upwards, a cone is formed with height h and volume V. The relationship between d, h, and V is represented above. Which of the following statements must be true ?
I. As the volume of the cone decreases, the height also decreases.
II. If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by 3π.
III. If the height of the conc triples, the volume must also triple.View SolutionA cylinder has a volume of 72π cubic inches and a height of 8 inches. If the height is increased by 4 inches, what will be the new volume of the cylinder in cubic inches?
View Solution

