D is the distance from vertex F to vertex G. The base is square, and the height is twice the width. What is the volume of the solid in terms of d ?
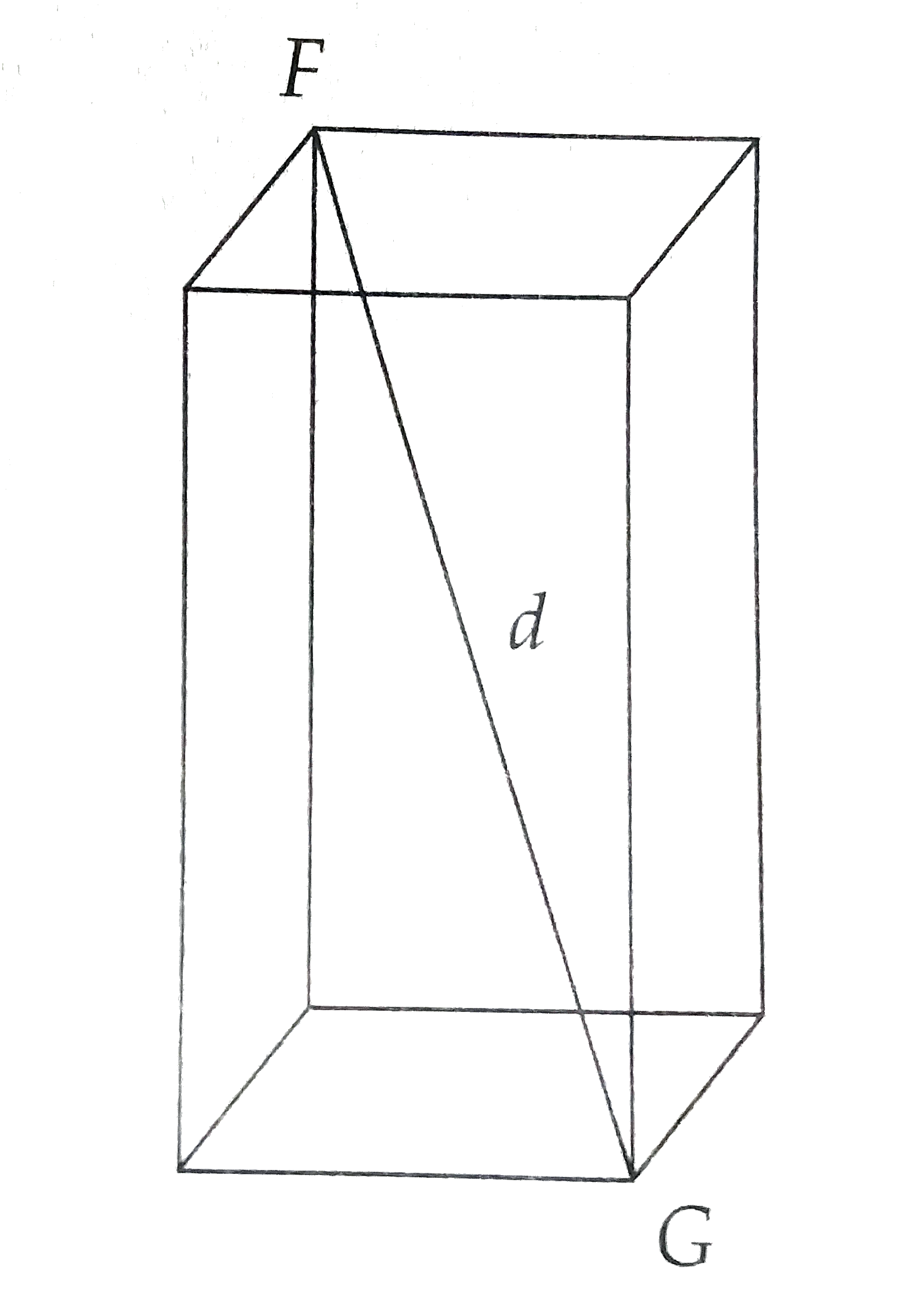
12d3√6
10d3√5
6d3√2
d3√618
The correct Answer is:D
Let the length and width be x and the height be 2x. Solve for x in terms of d.
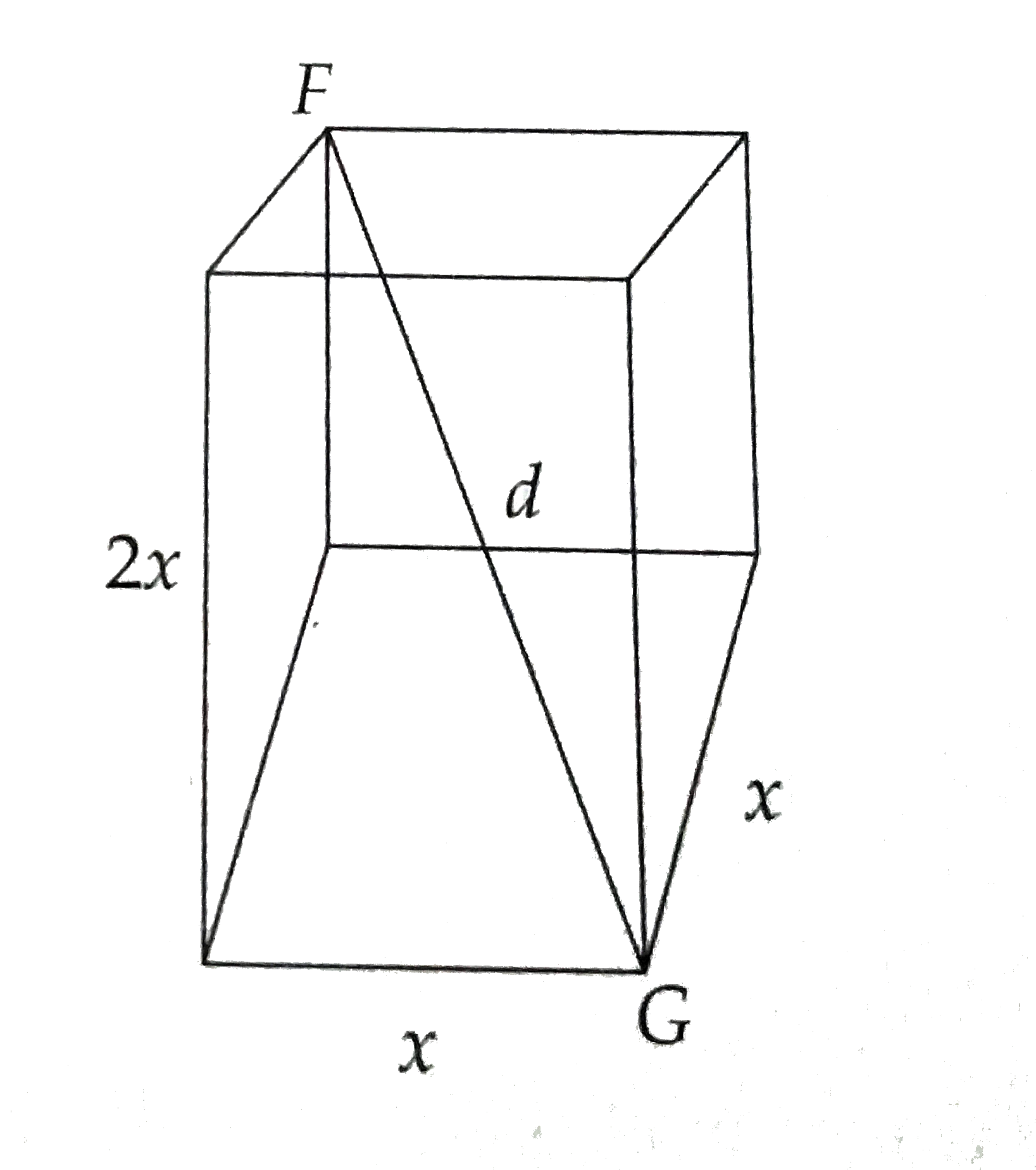
Use the formula for the distance between opposite vertices :
d=√l2+w2+h2
d=√x2+x2+(2x)2=√6x2=√6x
x=d√6
So for the dimensions of the solid we have l=w=d√6,h=2d√6.
Volume =l×w×h=(d√6)(d√6)(2d√6)
=2d36√6
=d33√6
=d33√6×√6√6
=d3√618
You also could Pick Numbers on this problem. Choose a value for x and then find the volume and the value of d. Plug d into the answer choices and see which one matches.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - SOLID GEOMETRY EXERCISE - SOLID GEOMETRY FOLLOW - UP TEST5videos
SOLID GEOMETRY
- BOOK - KAPLANCHAPTER - SIMILARITY, CONGRUENCE, AND PROOFSEXERCISE - Multiple Choice Question10videos
SIMILARITY, CONGRUENCE, AND PROOFS
- BOOK - KAPLANCHAPTER - SYSTEM OF LINEAR EQUATION EXERCISE - Multiple Choice Question20videos
SYSTEM OF LINEAR EQUATION
Similar Questions
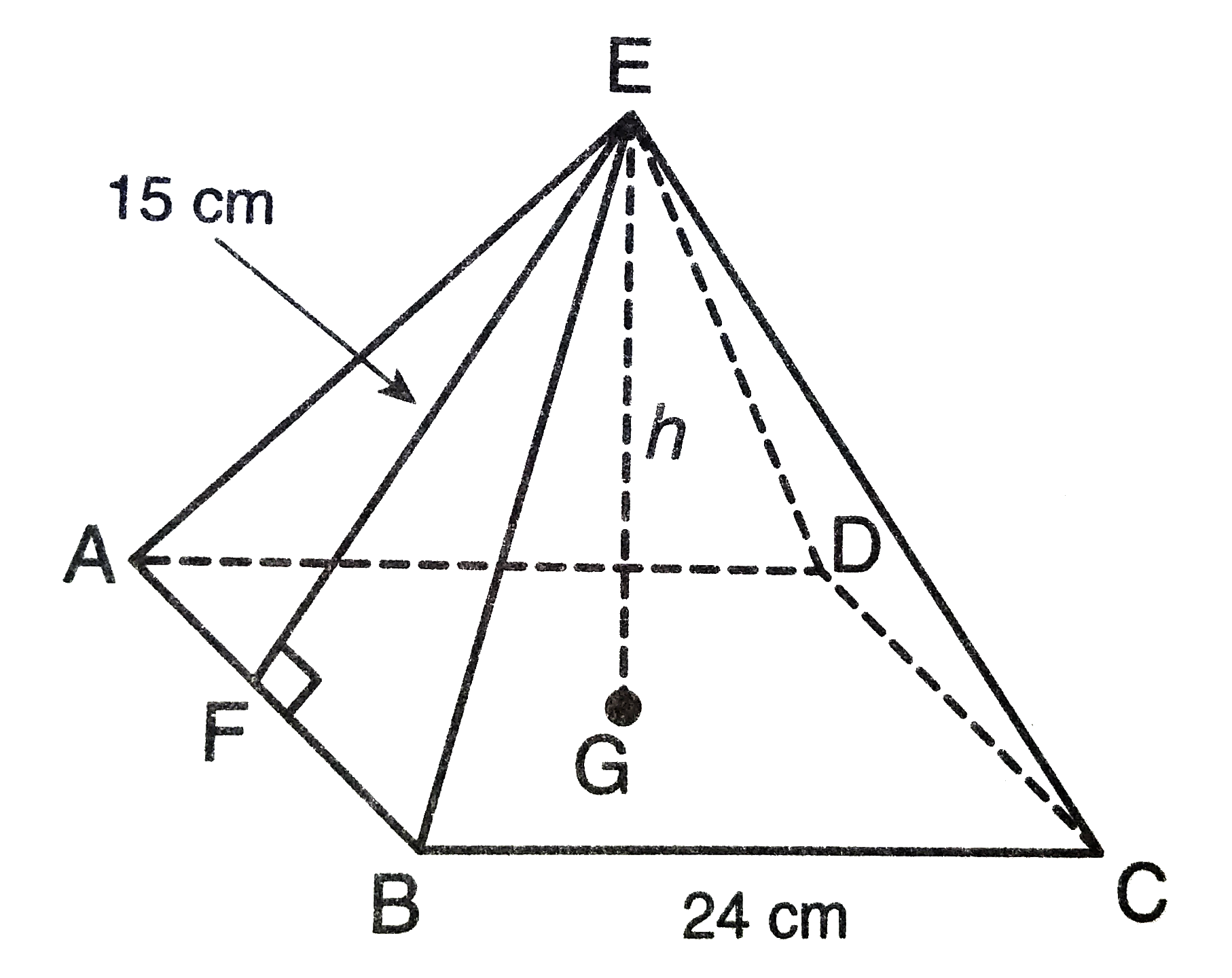
The slant height of a pyramid is the perpendicular distance from the vertex of the pyramid to the base of a figure above, the height is labeled h, the length of a side of the square base is 24 cm, and the slant height is 15 cm, What is the volume , in cubic centimeters, of the pyramid?View SolutionConsider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
 Aλ2.472Bλ2.236Cλ1.227Dλ3.412
Aλ2.472Bλ2.236Cλ1.227Dλ3.412 - Question 2 - Select One
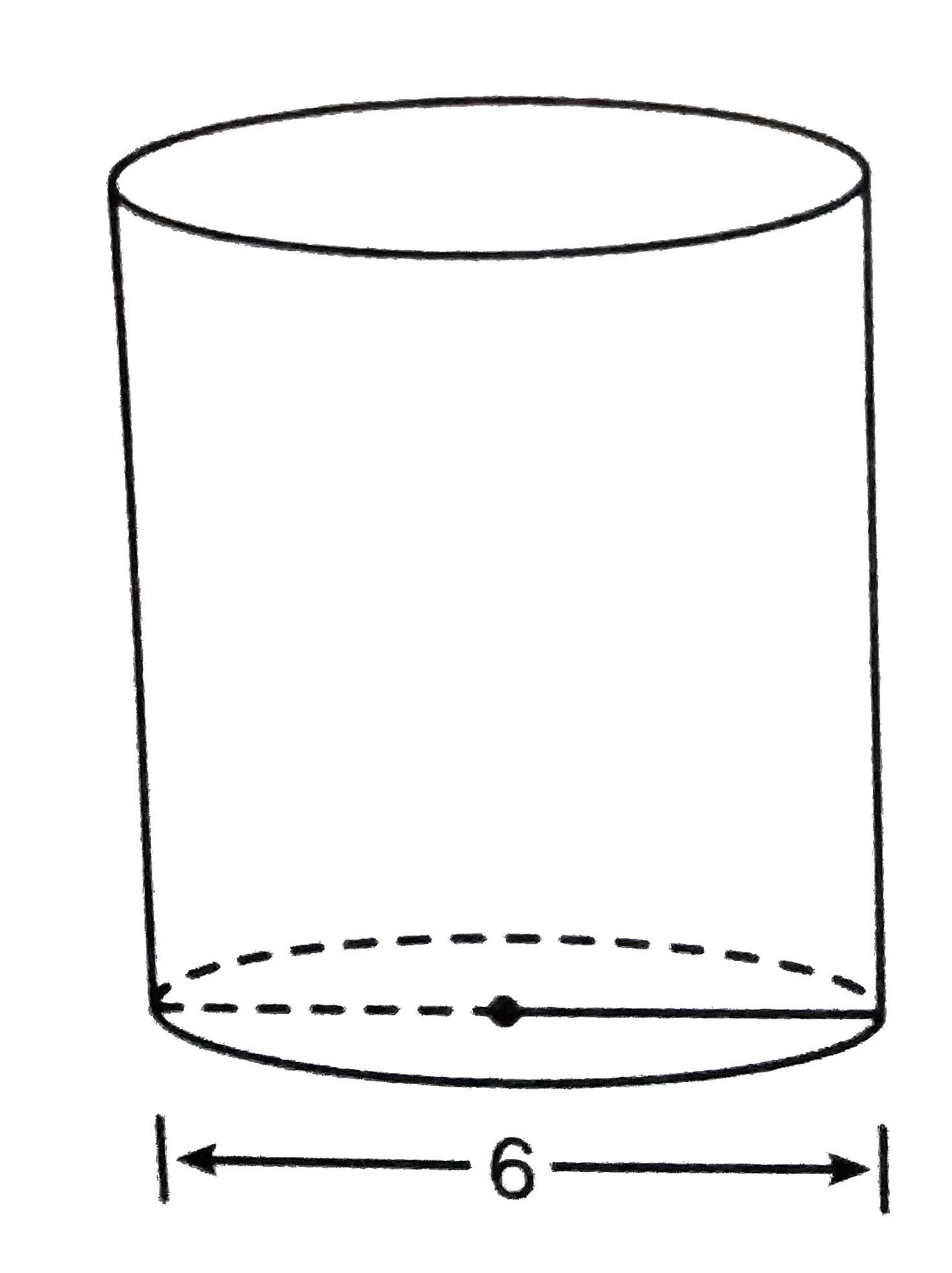
The diameter of the base of a right circular cylinder is 6 and the distance from the centre of a base to a point on the circumference of the other base is 8 what is the height of the cylinder?A2B10C√10D√55 - Question 3 - Select One
A cylinder has volume V, height h, and base diameter d. Which of the following represents d in terms of V and h?
Ad=√VπhBd=√vπhCd=√2VπhDd=√4Vπh
ABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
View SolutionABCD is a square of side l. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at x=1/√2 and at x=2, when l=2.
View SolutionA solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h . If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is (a) 2h (b) 2h3 (c) 3h2 (d) 4h
View SolutionA square has one vertex at the vertex of the parabola y2=4ax and the diagonal through the vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of the vertices of the square are (a)(4a,4a) (b) (4a,−4a) (c)(0,0) (d) (8a,0)
View SolutionFrom a solid circular cylinder with height 10 cm and radius of the base 6 cm, a circular cone of the same height and same base is removed. Find the volume of remaining solid and also find the whole surface area.
View Solution

