Two sides of a triangle measure 4 and 12. Which of the following could equal the length of the third side?
5
7
9
20
The correct Answer is:C
To determine which of the given options could be the length of the third side of a triangle with two sides measuring 4 and 12, we will use the triangle inequality theorem. This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
1. Identify the sides of the triangle:
We have two sides of the triangle: a=4 and b=12. We need to find the possible length of the third side c.
2. Apply the triangle inequality theorem:
According to the triangle inequality theorem, we have three conditions to check:
- a+b>c
- a+c>b
- b+c>a
3. Check each option one by one:
Option 1: c=5
- Check 4+5>12:
9>12 (False)
- Since this condition is false, 5 cannot be the length of the third side.
Option 2: c=7
- Check 4+7>12:
11>12 (False)
- Since this condition is false, 7 cannot be the length of the third side.
Option 3: c=9
- Check 4+9>12:
13>12 (True)
- Check 4+12>9:
16>9 (True)
- Check 12+9>4:
21>4 (True)
- All conditions are satisfied, so 9 can be the length of the third side.
Option 4: c=20
- Check 4+20>12:
24>12 (True)
- Check 4+12>20:
16>20 (False)
- Since this condition is false, 20 cannot be the length of the third side.
4. Conclusion:
After checking all options, only option 3 (9) satisfies the triangle inequality conditions. Therefore, the length of the third side can be 9.
We have two sides of the triangle: a=4 and b=12. We need to find the possible length of the third side c.
According to the triangle inequality theorem, we have three conditions to check:
- a+b>c
- a+c>b
- b+c>a
- Check 4+5>12:
9>12 (False)
- Since this condition is false, 5 cannot be the length of the third side.
- Check 4+7>12:
11>12 (False)
- Since this condition is false, 7 cannot be the length of the third side.
- Check 4+9>12:
13>12 (True)
- Check 4+12>9:
16>9 (True)
- Check 12+9>4:
21>4 (True)
- All conditions are satisfied, so 9 can be the length of the third side.
- Check 4+20>12:
24>12 (True)
- Check 4+12>20:
16>20 (False)
- Since this condition is false, 20 cannot be the length of the third side.
After checking all options, only option 3 (9) satisfies the triangle inequality conditions. Therefore, the length of the third side can be 9.
Similar Questions
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
View SolutionTwo sides of a triangle are 4 cm and 10 cm. what is the possible range of length of the third side ?
View SolutionIf two side of a triangle are ˆi+2ˆjandˆi+ˆk , then find the length of the third side.
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View SolutionTwo sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionThe lengths of two sides of a triangle are 6 cm and 8 cm. Between whichtwo numbers can length of the third side fall?
View SolutionTwo sides of a triangle are 15cm and 20cm. The perimeter of the triangle is 50cm. What is the third side?
View SolutionFind the length of the third side of the triangle.
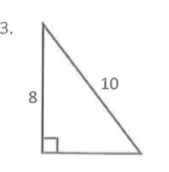
View SolutionFind the length of the third side of the triangle.
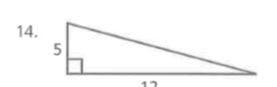
View SolutionIf two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
View Solution
