The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
To find the possible lengths of the third side of a triangle when the lengths of the other two sides are given, we can use the triangle inequality theorem. According to this theorem, the length of any side of a triangle must be less than the sum of the lengths of the other two sides and greater than the absolute difference of the lengths of the other two sides.
1. Identify the lengths of the two sides:
- Let the lengths of the two sides be a=12 cm and b=15 cm.
2. Apply the triangle inequality theorem:
- The length of the third side c must satisfy the following inequalities:
- c<a+b
- c>|a−b|
3. Calculate the sum of the two sides:
- a+b=12+15=27
- Therefore, c<27.
4. Calculate the absolute difference of the two sides:
- |a−b|=|12−15|=3
- Therefore, c>3.
5. Combine the results:
- From the inequalities, we have:
- 3<c<27
Conclusion:
The length of the third side c must fall between 3 cm and 27 cm.
- Let the lengths of the two sides be a=12 cm and b=15 cm.
- The length of the third side c must satisfy the following inequalities:
- c<a+b
- c>|a−b|
- a+b=12+15=27
- Therefore, c<27.
- |a−b|=|12−15|=3
- Therefore, c>3.
- From the inequalities, we have:
- 3<c<27
The length of the third side c must fall between 3 cm and 27 cm.
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.5
8 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.1
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - SOLVED EXAMPLES
6 Videos
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.2
2 Videos
Similar Questions
Knowledge Check
Two sides of a triangle measure 4 and 12. Which of the following could equal the length of the third side?
A5B7C9D20
Two sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionTwo sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
View SolutionThe length of one side of a right triangle is 24 cm and the length of its hypotenuse is 40 cm. Find the length of its third side.
View SolutionIf two side of a triangle are ˆi+2ˆjandˆi+ˆk , then find the length of the third side.
View SolutionFind the length of the third side of the triangle.
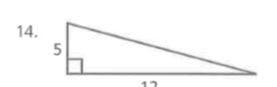
View SolutionFind the length of the third side of the triangle.
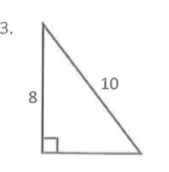
View SolutionTwo sides of a triangle have lengths of 8 and 17. What is the range of possible vlaus of the length of the thrid side?
View Solution
