If A, B, C, D and E are points in a plane such that line CD bisects ∠ACB and line CB bisects right angle ∠ACE, then ∠DCE =
22.5∘
45∘
575∘
67.5∘
The correct Answer is:D
To solve the problem, we need to analyze the given information about the angles and the points in the plane.
Step 1: Draw the Configuration
We start by placing the points A, B, C, D, and E in a plane. We can visualize the points as follows:
- Place point C at the origin (0,0).
- Point A is located such that angle ACB is formed.
- Point B is positioned such that angle ACB is formed.
- Point E is positioned such that angle ACE is a right angle (90 degrees).
- Point D lies on line segment CB.
Step 2: Identify the Angles
From the problem, we know:
- Line CD bisects angle ACB.
- Line CB bisects angle ACE, which is a right angle (90 degrees).
Step 3: Calculate Angles
1. Since line CB bisects angle ACE, we have:
∠ACB=∠BCE=12×90∘=45∘
2. Since line CD bisects angle ACB, we have:
∠ACD=∠DCB=12×∠ACB=12×45∘=22.5∘
Step 4: Find Angle DCE
Now we need to find angle DCE:
∠DCE=∠DCB+∠BCE
From our calculations:
- ∠DCB=22.5∘
- ∠BCE=45∘
Thus,
∠DCE=22.5∘+45∘=67.5∘
Final Answer
The value of angle DCE is:
∠DCE=67.5∘
We start by placing the points A, B, C, D, and E in a plane. We can visualize the points as follows:
- Place point C at the origin (0,0).
- Point A is located such that angle ACB is formed.
- Point B is positioned such that angle ACB is formed.
- Point E is positioned such that angle ACE is a right angle (90 degrees).
- Point D lies on line segment CB.
From the problem, we know:
- Line CD bisects angle ACB.
- Line CB bisects angle ACE, which is a right angle (90 degrees).
1. Since line CB bisects angle ACE, we have:
∠ACB=∠BCE=12×90∘=45∘
∠ACD=∠DCB=12×∠ACB=12×45∘=22.5∘
Now we need to find angle DCE:
∠DCE=∠DCB+∠BCE
From our calculations:
- ∠DCB=22.5∘
- ∠BCE=45∘
∠DCE=22.5∘+45∘=67.5∘
The value of angle DCE is:
∠DCE=67.5∘
Similar Questions
Knowledge Check
A, B,C and D are points on a line such that point B biscets line AC and point A bisects line CD. What is the ratio of AB to CD ?
A1/4B1/3C1/2D2/3In the figure, if line CE bisects ∠ACB then x =
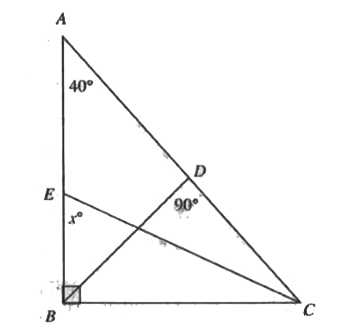 A45B50C55D65
A45B50C55D65
If lines AB,AC,AD and AE are parallel to a line l show that points A,B,C,D and E are collinear.
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionD, E and F are the points on sides BC, CA and AB respectively of ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C . If AB=5cm, BC=8cm and CA=4cm , determine AF, CE and BD .
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠Bas well as ∠D.
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2 .
View Solution
