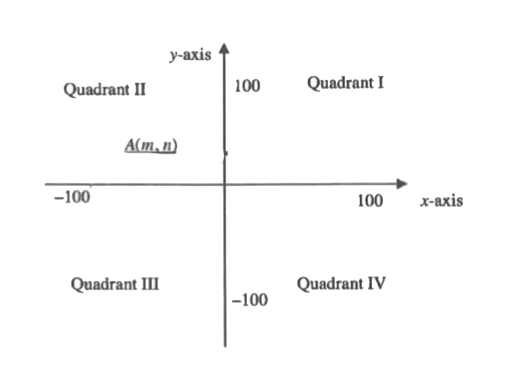
In the figure, the point A(m, n) lies in Quadrant II as shown. In which region is the point $B (n, m)$ ?

Quadrant I

Quadrant II

Quadrant IV

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Answer

Step by step video, text & image solution for In the figure, the point A(m, n) lies in Quadrant II as shown. In which region is the point B(n, m)? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Knowledge Check

Question 1 - Select One

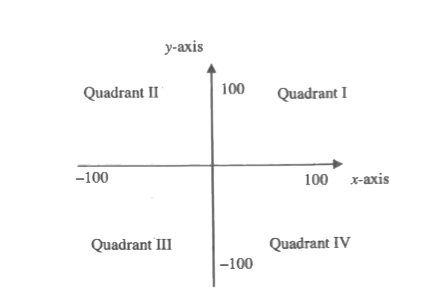
In the coordinates system shown, if (b, a) lies in Quadrant III, then in which quadrant can the point (a, b) lie?
AI only
BII only
CIII only
DIV only
Question 2 - Select One
If the point (a,b) is in Quadrant II and $| a | - | b | > 0$ , then which one of the following is true?
A $a > 0$
B $b > 0$
C $a > b$
D $a + b < 0$

Let $m, n$ are integers with $0 < n < m .$ A is the point $(m, n)$ on the Cartesian plane. $B$ is the reflection of $A$ in the line $y = x .$ $C$ is the reflection of $B$ in the y-axis. $D,$ is the reflection of $C$ in the x-axis and $E$ is the reflection of $D$ in the y-axis. The area of the pentagon $A B C D E$ is $2 m (m + n)$ (b) $m (m + 3 n)$ $m (2 m + 3 n)$ (d) $2 m (m + 3 n)$
View Solution
At the point $P (a, a^{n})$ on the graph of $y = x^{n}, (n \in N)$ , in the first quadrant, a normal is drawn. The normal intersects the $y$ - $a ξ s$ at the point $(0, b)$ . If ${(lim)}_{a \to 0} = \frac{1}{2},$ then $n$ equals _____.
View Solution
Let $m, n$ are integers with $0 < n < m$ . A is the point $(m, n)$ on the Cartesian plane. $B$ is the reflection of $A$ in the line $y = x$ . $C$ is the reflection of $B$ in the y-axis, $D$ is the reflection of $C$ in the x-axis and $E$ is the reflection of $D$ in the y-axis. The area of the pentagon $A B C D E$ is
a. $2 m (m + n)$ b. $m (m + 3 n)$ c. $m (2 m + 3 n)$ d. $2 m (m + 3 n)$
View Solution
At the point $P (a, a^{n})$ on the graph of $y = x^{n} (n \in N)$ in the first quadrant at normal is drawn. The normal intersects the Y-axis at the point (0, b). If $lim a \to 0 b = \frac{1}{2}$ , then n equals ……………
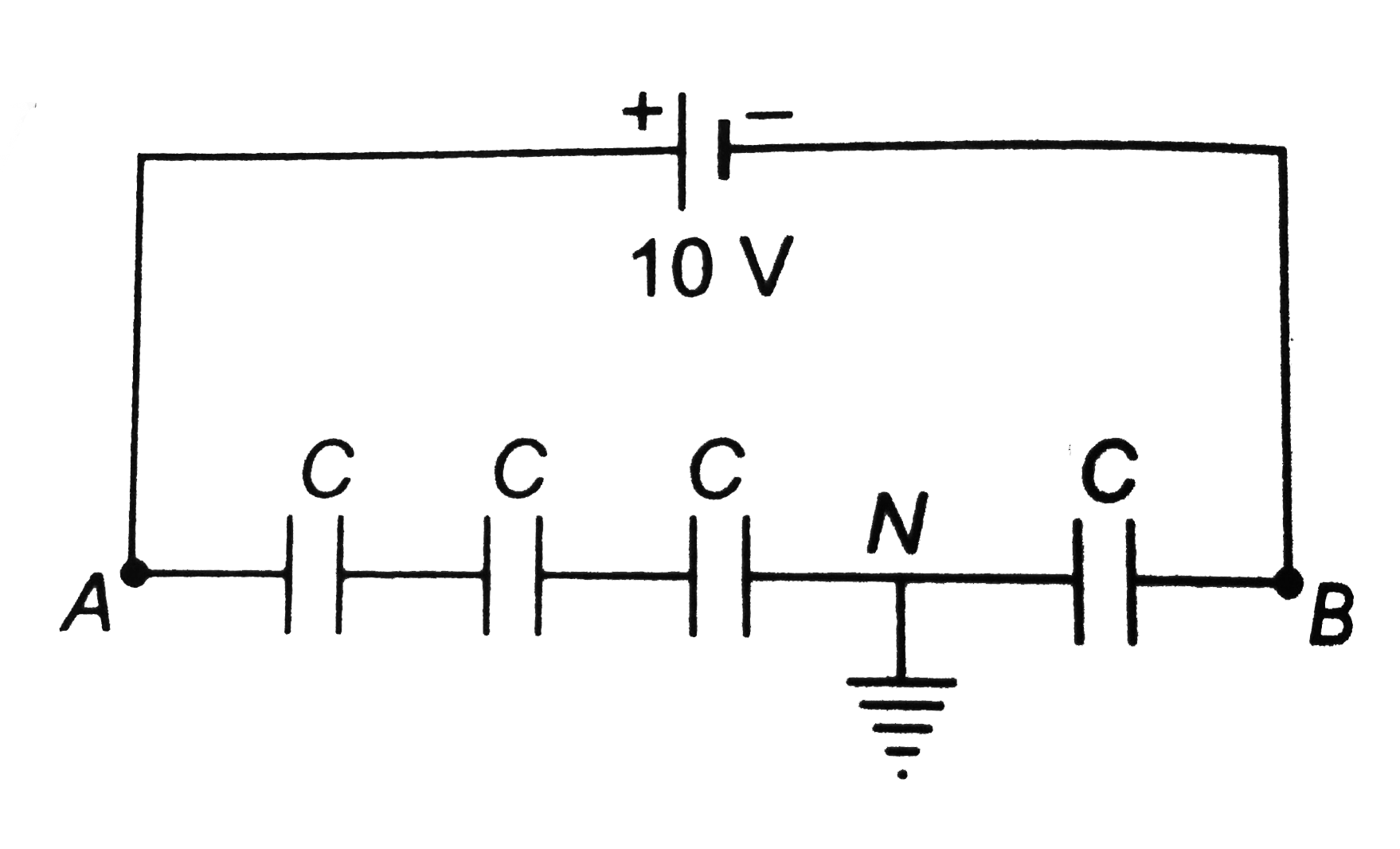
View Solution
Four identical capacitors are connected in series with a $10 V$ battery as shown in the figure. The point $N$ is earthed. The potentials of points $A$ and $B$ are

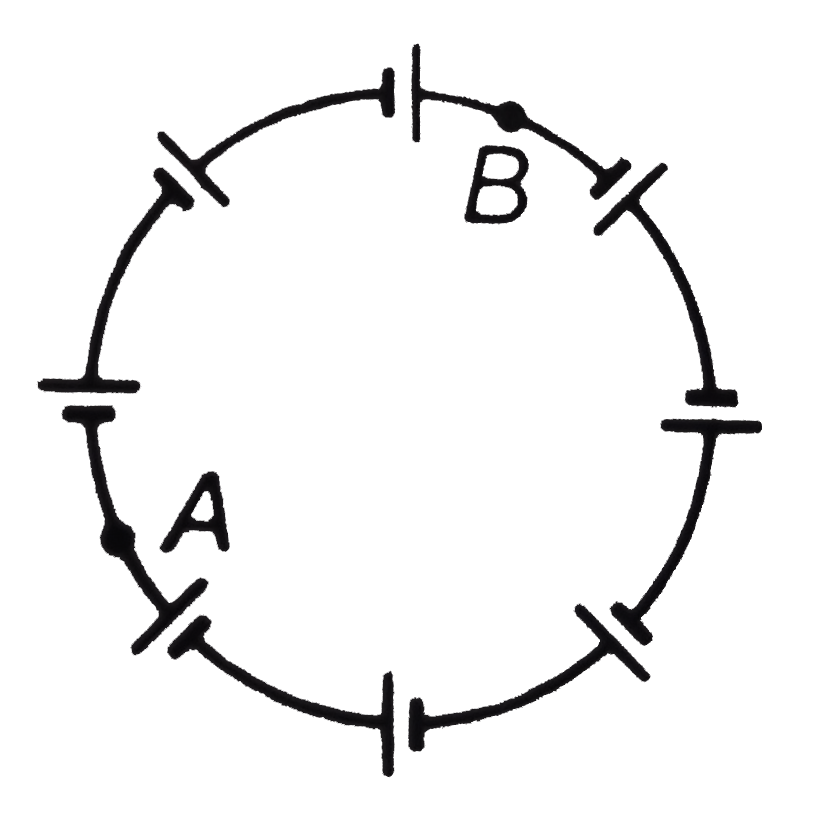
View Solution
N identical current sources each of emf E and internal resistance r are connected to form a closed loop as shown in figure. The potential difference between points A and B which divides the circuit into n and (N-n) units is

View Solution

In the figure, the point A(m, n) lies in Quadrant II as shown. In which region is the point $B (n, m)$ ?

The correct Answer is:D

Similar Questions

Knowledge Check

In the coordinates system shown, if (b, a) lies in Quadrant III, then in which quadrant can the point (a, b) lie?

If the point (a,b) is in Quadrant II and $| a | - | b | > 0$ , then which one of the following is true?

Recommended Questions

In the figure, the point A(m, n) lies in Quadrant II as shown. In which region is the point B(n,m)?

The correct Answer is:D

Similar Questions

Knowledge Check

In the coordinates system shown, if (b, a) lies in Quadrant III, then in which quadrant can the point (a, b) lie?

If the point (a,b) is in Quadrant II and |a|−|b|>0, then which one of the following is true?

Recommended Questions

In the figure, the point A(m, n) lies in Quadrant II as shown. In which region is the point $B (n, m)$ ?

If the point (a,b) is in Quadrant II and $| a | - | b | > 0$ , then which one of the following is true?