The block shown in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

Consider the block + the part of the string below A as the system . Let the tension at A be T. The forces acting on this system are
a. (M+mg) g, downward, by the earth
T, upward, by the upper part of the string.
The first is gravitational and the second is electromagnetic. We do not have to write the force by the string on the block. This electromagnetic force is by one part of the system on the other part. Only the forces acting on the system by the objects other than the system are to be included.
The system is descending with an acceleration a. Taking the downward direction as the Y-axis, the total force along the X-axis is (M+m)g−T. Using Newton's law along the X-axis is (M+m)g−T=(M+m)a.
or T=(M+m)(g−a)...........(i)
we have omitted the free body diagram. This you can do if you can draw the free body diagram in your mind and write the equations correctly.
To get the tension T' at the lower end we can put m=0 in i.
Effectively we take the point A at the lower end. Thus, we get T'=M(g−a).
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples11videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -114videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
The mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View SolutionThe block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
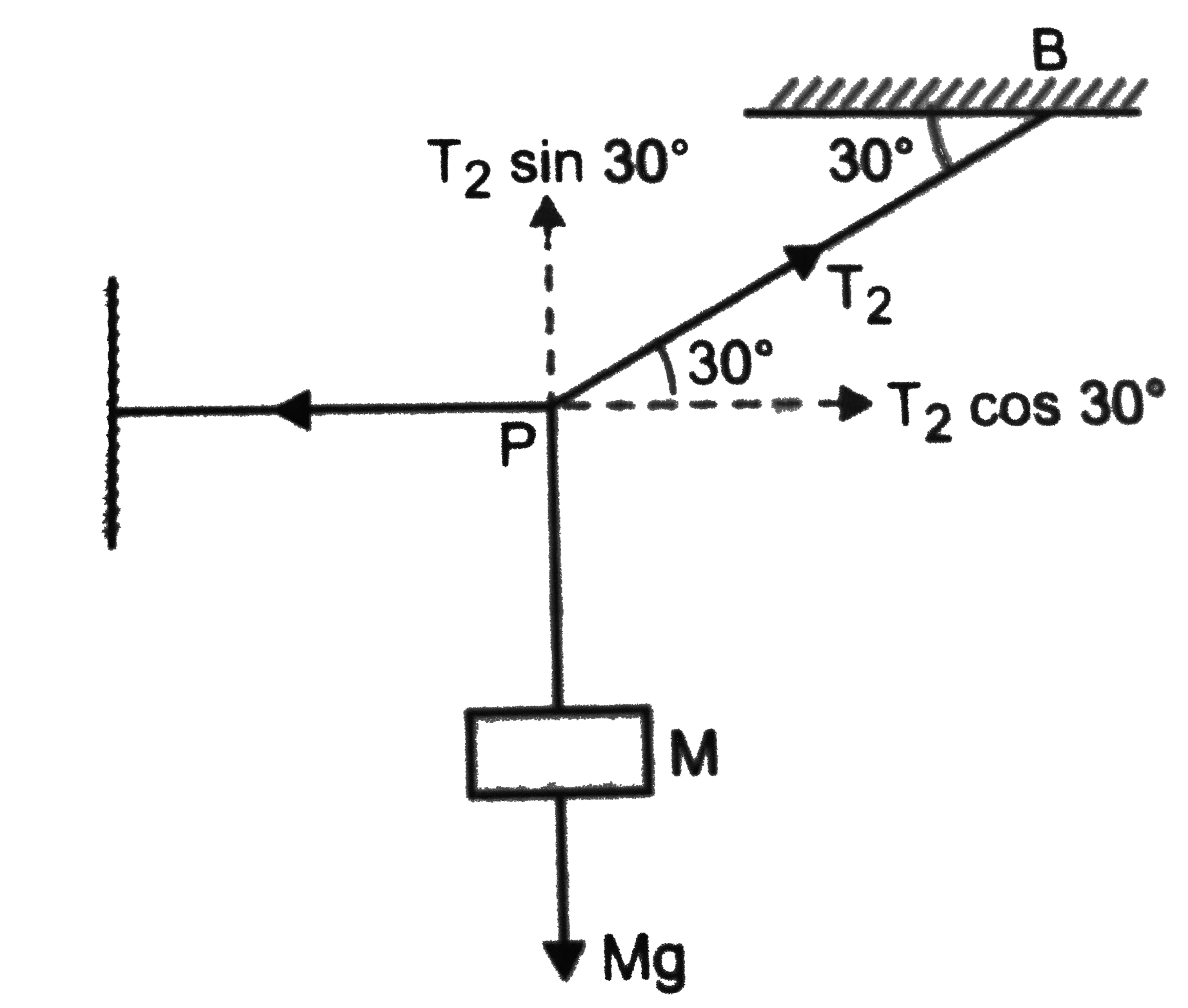 View Solution
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 View Solution
View SolutionA thin uniform bar of mass m and length 2L is held at an angle 30∘ with the horizontal by means of two vertical inextensible strings, at each end as shown in figure. If the string at the right end breaks, leaving the bar to swing, determine the tension in the string at the left end and the angular acceleration of the bar immediately after string breaks.
 View Solution
View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass m can slide on the string without any friction. One end of the string is attached to point B and to the other end, a block 'P' of mass m is attached. The whole system lies in vertical plane.
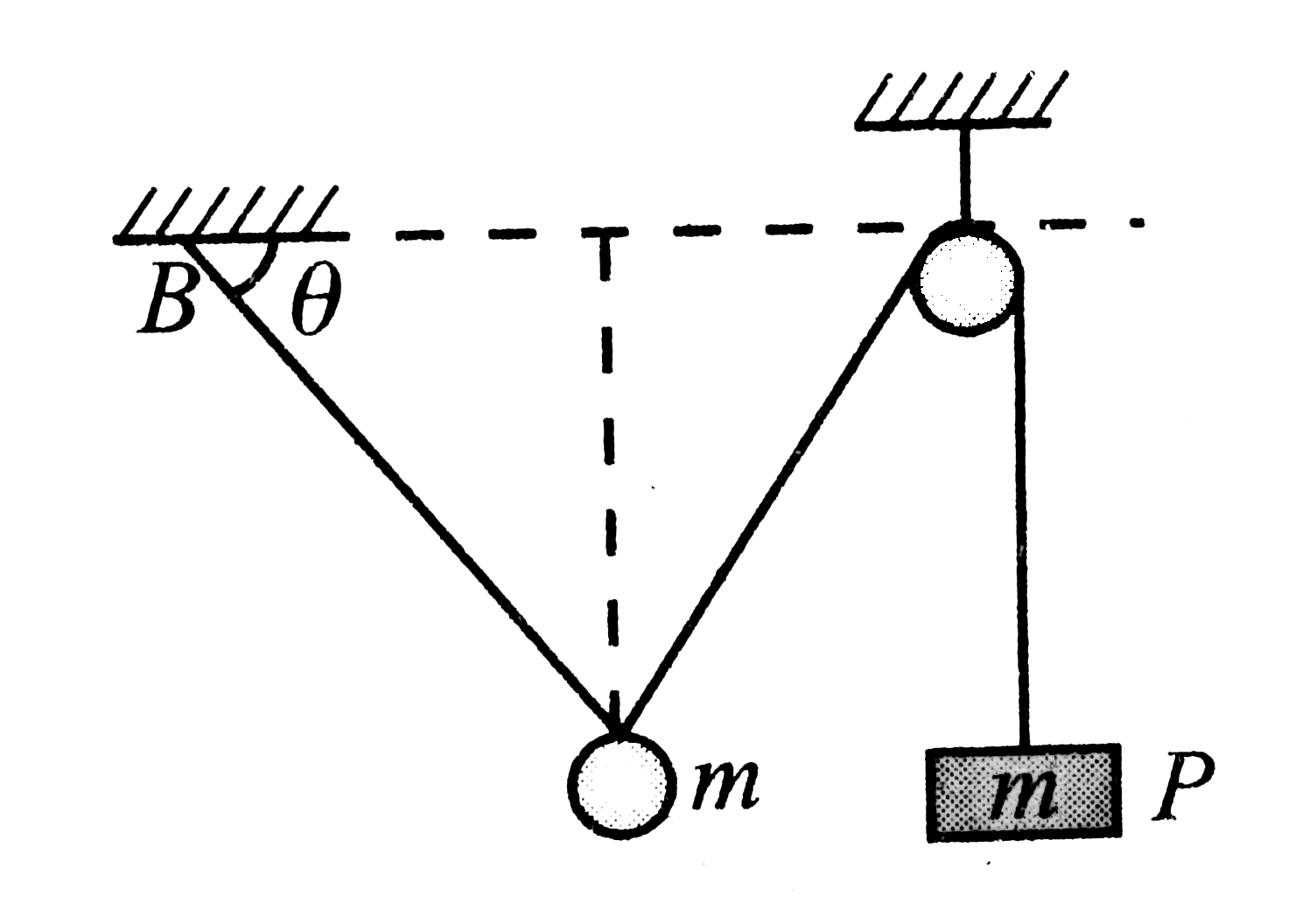 Now another block 'C' of same mass m is attached to the block 'P' and system is released from rest. If a1 and a2 are the magnitudes of initial accelerations of ring and blocks, respectively, then View Solution
Now another block 'C' of same mass m is attached to the block 'P' and system is released from rest. If a1 and a2 are the magnitudes of initial accelerations of ring and blocks, respectively, then View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
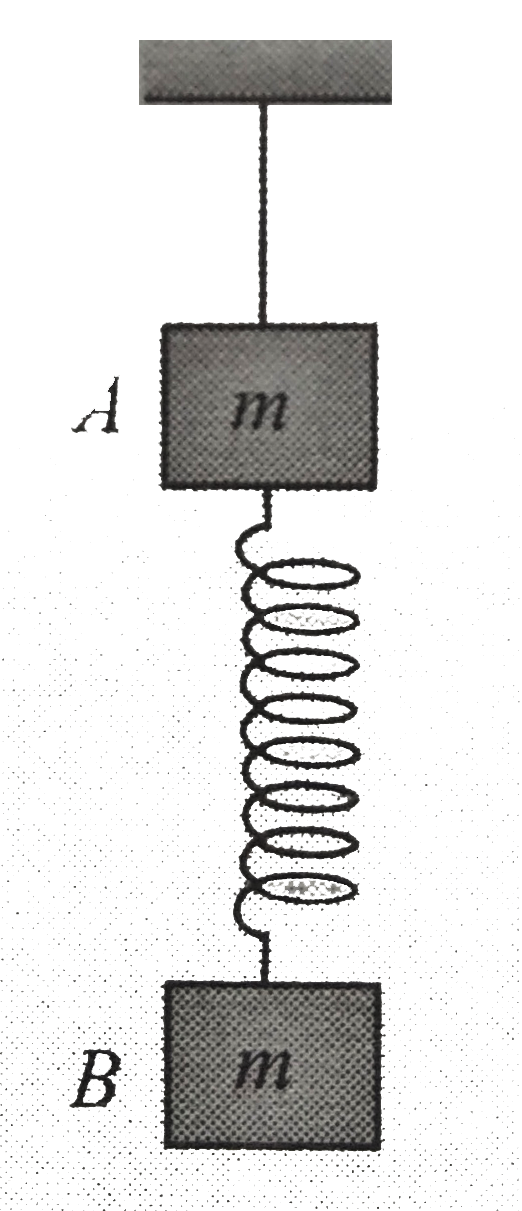 View Solution
View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.
 View Solution
View Solution

