While finding the Sine of a certain angle x, an absent minded professor failed to notice hat his calculator was not in the correct angular mode. However he was lucky to get the right answer. The two least positive values of x for which the Sine of x degrees is the same as the Sine of x radians were found by him as mπn−π and pπq+π where m,n , p and q are positive integers . Suppose mnpq be denoted by the quantity 'L'. Now answer the following questions.
If x is measured in radians and Limx→∞(√Ax2+Bx−Cx)=L, then the value of BCA equals( A,B,C∈R)
A
4
B
2
C
12
D
None of these
Text Solution
The correct Answer is:B
|
Topper's Solved these Questions
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-4
17 Videos
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-2(LEVEL-2)
5 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - MOTIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise -4 Level -II
7 Videos
- MATRICES BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)
28 Videos
Similar Questions
Knowledge Check
While finding the Sine of a certain angle x, an absent minded professor failed to notice hat his calculator was not in the correct angular mode. However he was lucky to get the right answer. The two least positive values of x for which the Sine of x degrees is the same as the Sine of x radians were found by him as mπn−π and pπq+π where m,n , p and q are positive integers . Suppose mnpq be denoted by the quantity 'L'. Now answer the following questions.
The value of (m+n+p+q) is equal toA720B900C1080D1260While finding the Sine of a certain angle x, an absent minded professor failed to notice hat his calculator was not in the correct angular mode. However he was lucky to get the right answer. The two least positive values of x for which the Sine of x degrees is the same as the Sine of x radians were found by him as mπn−π and pπq+π where m,n , p and q are positive integers . Suppose mnpq be denoted by the quantity 'L'. Now answer the following questions.
Assume that f(x) is differentiable for all x.The sign of f'(x) is as follows :
f'(x)>0 on (−∞,−4)
f'(x)<0 on (−4,6)
f'(x)>0 on (6,∞)
Let g(x) = f ( 10-2x ) . The value of g' ( L) isApositiveBnegativeCzeroDthe function g is not differentiable at x= 5If the sides of a right angled triangle are in A.P. then the sines of the acute angles are
A35,45B√3,13C√√5−12,√√5+12D√32,12
If the sides of a right angled triangle are in A.P then the sines of the acute angles are
View Solution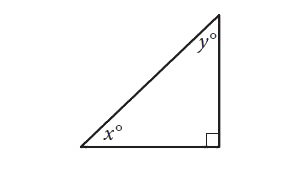
In the triangle above, the sine of x∘ is 0.6. What is the cosine of y∘ ?
View SolutionThe angles of a triangle are in AP and the ratio of the number of degrees in the least to the number of radians in the greatest is 60:π. Find the angles in degree and radians.
View SolutionWhat name is given to the ratio of sine of angle of incidence to the sine of angle of refraction?
View Solution(The tangents of two acute angles are 3 and 2, The sine of twice their difference is
View Solution
