A wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae−(tT−xλ)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave.
(b) find the function f(t) represent the displacement of particle at x=0.
(c ) Plot the function g(x) representing the shape of the string at t=0
(d) Plot the function g(x) of the string at t=0 and t=5 s
The wave equation may be written as
y=y0e−tT2{t−xλ/T}2
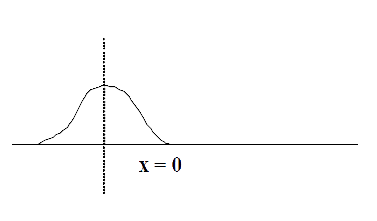
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Questions for practice12videos
SOUND WAVES
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 182videos
SOUND WAVES
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - EXERCISE - 4 ( LEVEL II)24videos
SOUND WAVES
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]11videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SURFACE TENSIONEXERCISE - Exercise - 3 | Section - B Previous Year Problems | AIEEE12videos
SURFACE TENSION
Similar Questions
A wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae(−tt−xA)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 sView SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.View Solution
Knowledge Check
- Question 1 - Select One
If the wave equation y=0.08sin(2π)λ(200t−x) then the velocity of the wave will be
A400√2B200√2C400D200 - Question 2 - Select One
The equation of a wave is y=5sin(t0.04−x4) where x is in cm and t is in seccond. The velocity of the wave will be
A1ms−1B2ms−1C1.5ms−1D1.25ms−1 - Question 3 - Select One
The displacement of a particle of a string carrying a travelling wave is given by y = (3 cm) sin 6.28 (0.50 x – 50 t) where x is in centimeter and t is in second. The velocity of the wave is-
A100 m/sB50 cm/sC100 cm/sD10 m/s
A wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(ii) Shape of the pulse at t = 0 and t = 1s.View SolutionA wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View SolutionThe displacement function of a wave traveling along positive x-direction is y=12+2x2 at t=0and by y=12+2(x−2)2 at t=2s, where y and x are in metre. The velocity of the wave is:
View Solution

