Statement (1) : If a and b are integers and roots of $x^{2} + a x + b = 0$ are rational then they must be integers. Statement (2): If the coefficient of $x^{2}$ in a quadratic equation is unity then its roots must be integers

Video Solution

Answer

Step by step video & image solution for Statement (1) : If a and b are integers and roots of x^2 + ax + b = 0 are rational then they must be integers. Statement (2): If the coefficient of x^2 in a quadratic equation is unity then its roots must be integers by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DEFAULT

Knowledge Check

If the roots of $x^{2} - a x + b = 0$ are two consecutive odd integers, then $a^{2} - 4 b$ is equal to
A3
B4
C5
D6

Suppose a, b are integers and a + b is a root of $x^{2} + a x + b = 0$ . What is the maximum possible values of $b^{2}$ ?
View Solution
If a, b, c are distanct integers and $w \neq 1$ is a cube root of unity, then

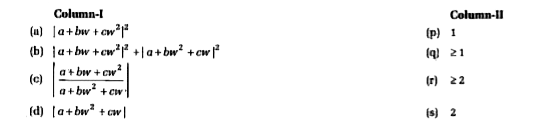
View Solution
If $a, b, a n d c$ are odd integers, then prove that roots of $a x^{2} + b x + c = 0$ cannot be rational.
View Solution
If the roots of the equation $x^{2} - b x + c = 0$ are two consecutive integers then $3 (b^{2} - 4 c) =$
View Solution
If a and b are the odd integers, then the roots of the equation, $2 a x^{2} + (2 a + b) x + b = 0, a \neq 0$ , will be
View Solution
Statement 1: If $a, b, c$ are all rational and one of the roots of the equation $a x^{2} + b x + c = 0$ is $2 - \sqrt{5}$ then the other root is $2 + \sqrt{5}$ . Statement 2: In any quadratic equation with rational coefficients, the irrational roots always occur in the conjugate pair.
View Solution
Statement -1 : A root of the equation $(2^{10} - 3) x^{2} - 2^{11} x + 2^{10} + 3 = 0 is 1$
and
Statement-2 : The sum of the coefficients of a quadratic equation is zero, then 1 is a root of the equation.
View Solution

Statement (1) : If a and b are integers and roots of $x^{2} + a x + b = 0$ are rational then they must be integers. Statement (2): If the coefficient of $x^{2}$ in a quadratic equation is unity then its roots must be integers

Similar Questions

Knowledge Check

If the roots of $x^{2} - a x + b = 0$ are two consecutive odd integers, then $a^{2} - 4 b$ is equal to

Recommended Questions

Statement (1) : If a and b are integers and roots of x2+ax+b=0 are rational then they must be integers. Statement (2): If the coefficient of x2 in a quadratic equation is unity then its roots must be integers

Similar Questions

Knowledge Check

If the roots of x2−ax+b=0 are two consecutive odd integers, then a2−4b is equal to

Recommended Questions

Statement (1) : If a and b are integers and roots of $x^{2} + a x + b = 0$ are rational then they must be integers. Statement (2): If the coefficient of $x^{2}$ in a quadratic equation is unity then its roots must be integers

If the roots of $x^{2} - a x + b = 0$ are two consecutive odd integers, then $a^{2} - 4 b$ is equal to