The value of tan[12cos−1(√53)] is :
3+√52
3+√5
3−√52
None of these
The correct Answer is:C
To solve the problem tan(12cos−1(√53)), we can follow these steps:
Step 1: Let θ=cos−1(√53)
This means that cos(θ)=√53.
Step 2: Use the half-angle identity for tangent
We know that:
tan(θ2)=√1−cos(θ)1+cos(θ)
So, we can substitute cos(θ) into this identity.
Step 3: Substitute cos(θ) into the half-angle identity
Substituting cos(θ)=√53:
tan(θ2)=
⎷1−√531+√53
Step 4: Simplify the expression
First, simplify the numerator:
1−√53=3−√53
Now for the denominator:
1+√53=3+√53
Now substituting these back into the tangent expression:
tan(θ2)=
⎷3−√533+√53=√3−√53+√5
Step 5: Rationalize the denominator
To rationalize the denominator, multiply the numerator and denominator by 3−√5:
tan(θ2)=
⎷(3−√5)2(3+√5)(3−√5)
Calculating the denominator:
(3+√5)(3−√5)=9−5=4
Calculating the numerator:
(3−√5)2=9−6√5+5=14−6√5
Thus, we have:
tan(θ2)=√14−6√54=√14−6√52
Final Answer
The value of tan(12cos−1(√53)) is:
√14−6√52
This means that cos(θ)=√53.
We know that:
tan(θ2)=√1−cos(θ)1+cos(θ)
So, we can substitute cos(θ) into this identity.
Substituting cos(θ)=√53:
tan(θ2)=
⎷1−√531+√53
First, simplify the numerator:
1−√53=3−√53
Now for the denominator:
1+√53=3+√53
Now substituting these back into the tangent expression:
tan(θ2)=
⎷3−√533+√53=√3−√53+√5
To rationalize the denominator, multiply the numerator and denominator by 3−√5:
tan(θ2)=
⎷(3−√5)2(3+√5)(3−√5)
Calculating the denominator:
(3+√5)(3−√5)=9−5=4
Calculating the numerator:
(3−√5)2=9−6√5+5=14−6√5
Thus, we have:
tan(θ2)=√14−6√54=√14−6√52
The value of tan(12cos−1(√53)) is:
√14−6√52
Similar Questions
Knowledge Check
- Question 1 - Select One
Let the tangents at point P and R on the parabola y=x2 intersects at T. Tangent at point Q (lies in between the points P and R) on the parabola intersect PT and RT at A and B respectively. The value of TATP+TBTR is
A12B1C2D4 - Question 2 - Select One
If sin−1(2a)1+a2+sin−12b1+b2 then x is =2ta−1x,
equal toAa−b1+abBb1+abCb1−abDa+b1−ab - Question 3 - Select One
The value of (Cp−Cv) is 1.00R for a gas sample in state A and is 1.08 R in state B. Let (pA,pB)denote the pressures and (TAandTB) denote the temperatures of the states A and B respectively . Most likely
ApA<pB and TA>TBBpA>pBandTA<TBCpA=pBandTA<TBDpA>pBandTA=TB
Two gases of molecular masses MA and MB) are at temperatures TA and TB respectively.TAMB=TBMA Which one of the following properties has the same value for both gases? (A) Pressure (B) Kinetic energy (C) RMS velocity (D) Density
View SolutionA solenoid has an inductance of 10 H and a resistance R=5Ω . It is connected ta a 10 V battery . How long will be it take for the magnetic energy to reach 14 of its maximum value ?
View Solutionif the tangent ta the curve x=a(1+sinθ),y=a(1+cosθ) at θ=π3 makes an angle x=axis then α
View SolutionA ball is hanging vertically by a light inextensible string of length L from fixed point O. The ball of mass m is given a speed u at the lowest position such that it completes a vertical circle with centre at O as shown. Let AB be a diameter of circular path of ball making an angle θ with vertical as shown. (g is acceleration due to gravity)
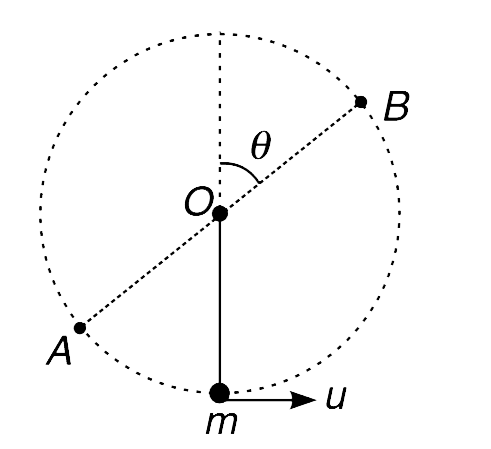
a) Let TA and TB be tension in string when ball is at A and B respectively, then find TA – TB. (b) Let →aA and →aB be acceleration of ball when it is at A and B respectively, then find the value of |→aA+→aB|View Solutionlimx→0xtan2x−2xtanx(1−cos2x)2 is
View Solution

