ABCD is a trapezium such that $A B ∣ ∣ C D a n d C B$ is perpendicular to them. If $∠ A D B = θ, B C = p, a n d C D = q$ , show that $A B = \frac{(p^{2} + q^{2}) sin θ}{p cos θ + q sin θ}$

Video Solution

Answer

Step by step video & image solution for ABCD is a trapezium such that A B||C Da n dC B is perpendicular to them. If /_A D B=theta,B C=p ,a n dC D=q , show that A B=((p^2+q^2)sintheta)/(pcostheta+qsintheta) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS TRIGONOMETRIC FUNCTIONS

Similar Questions

ABCD is a trapezium such that $A B ∣ ∣ C D a n d C B$ is perpendicular to them. If $∠ A D B = θ, B C = p, a n d C D = q$ , show that $A B = \frac{(p^{2} + q^{2}) sin θ}{p cos θ + q sin θ}$
View Solution
ABCD is a trapezium such that AB and CD are parallel and $B C ⊥ C D$ . If $∠ A D B = θ, B C = p a n d C D = q$ , then AB is equal to (1) $\frac{p^{2} + q^{2} cos θ}{p cos θ + q sin θ}$ (2) $\frac{p^{2} + q^{2}}{p^{2} cos θ + q^{2} sin θ}$ (3) $\frac{(p^{2} + q^{2}) sin θ}{{(p cos θ + q sin θ)}^{2}}$ (4) $\frac{(p^{2} + q^{2}) sin θ}{p cos θ + q sin θ}$
View Solution
ABCD is a trapezium in which $A B ∣ ∣ D C$ and $∠ A = ∠ B = 40^{\circ}$ . Find $∠ C$ and $∠ D$ . Are these angles equal?
View Solution
ABCD is a trapezium in which $A B ∣ ∣ D C$ $∠ A = ∠ B = 30 d e g r e e$ . Find $∠ C$ and $∠ D$ . Are these angles equal?

View Solution
$A B C D$ is a trapezium in which $A B D C$ . $P$ and $Q$ are points on sides $A D$ and $B C$ such that $P Q A B$ . If $P D = 18$ , $B Q = 35$ and $Q C = 15$ , find $A D$ .
View Solution
If $p sin θ + q cos θ = 3 & q sin θ - p cos θ = 2$ , then $p^{2} + q^{2} = ?$
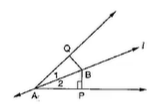
View Solution
In Figure, line $l$ is the bisector of angle $A a n d B$ is any point on $l . B P a n d B Q$ are perpendiculars from $B$ to the arms of $A .$ Show that: $A P B ≅ A Q B$ BP=BQ or B is equidistant from the arms of $∠ A$

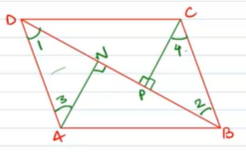
View Solution
In Figure, $A N$ and $C P$ are perpendicular to the diagonal $B D$ of a parallelogram $A B C D .$ Prove that : $A D N ≅ C B P$ (ii) $A N = C P$

View Solution
$A B C D$ is a cyclic quadrilateral whose diagonals $A C a n d B D$ intersect at $P$ . If $A B = D C,$ Prove that : $P A B ≅ P D C$ $P A = P D a n d P C = P B$ $A D B C$
View Solution
line l is the bisector of an angle $∠ A a n d ∠ B$ is any point on l. BP and BQ are perpendiculars from B to the arms of $∠ A$ . Show that:
(i) $Δ A P B ≅ Δ A Q B$
(ii) BP = BQ or B is equidistant from the arms of $∠ A$

View Solution

ABCD is a trapezium such that AB∣∣CDandCB is perpendicular to them. If ∠ADB=θ,BC=p,andCD=q , show that AB=(p2+q2)sinθpcosθ+qsinθ

Similar Questions

Recommended Questions

ABCD is a trapezium such that $A B ∣ ∣ C D a n d C B$ is perpendicular to them. If $∠ A D B = θ, B C = p, a n d C D = q$ , show that $A B = \frac{(p^{2} + q^{2}) sin θ}{p cos θ + q sin θ}$