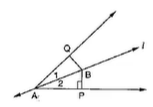
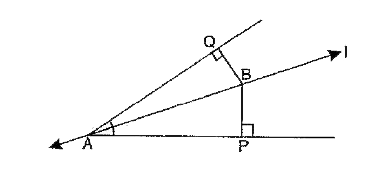
In Figure, line l
is the bisector of
angle A and B
is any point on l.BP and BQ
are perpendiculars from
B
to the arms of A.
Show that:
APB ≅AQB
BP=BQ or B is
equidistant from the arms of ∠A
Step by step video & image solution for In Figure, line l is the bisector of angle A\ a n d\ B is any point on ldotB P\ a n d\ B Q are perpendiculars from B to the arms of Adot Show that: A P B\ ~= A Q B BP=BQ or B is equidistant from the arms of /_A by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

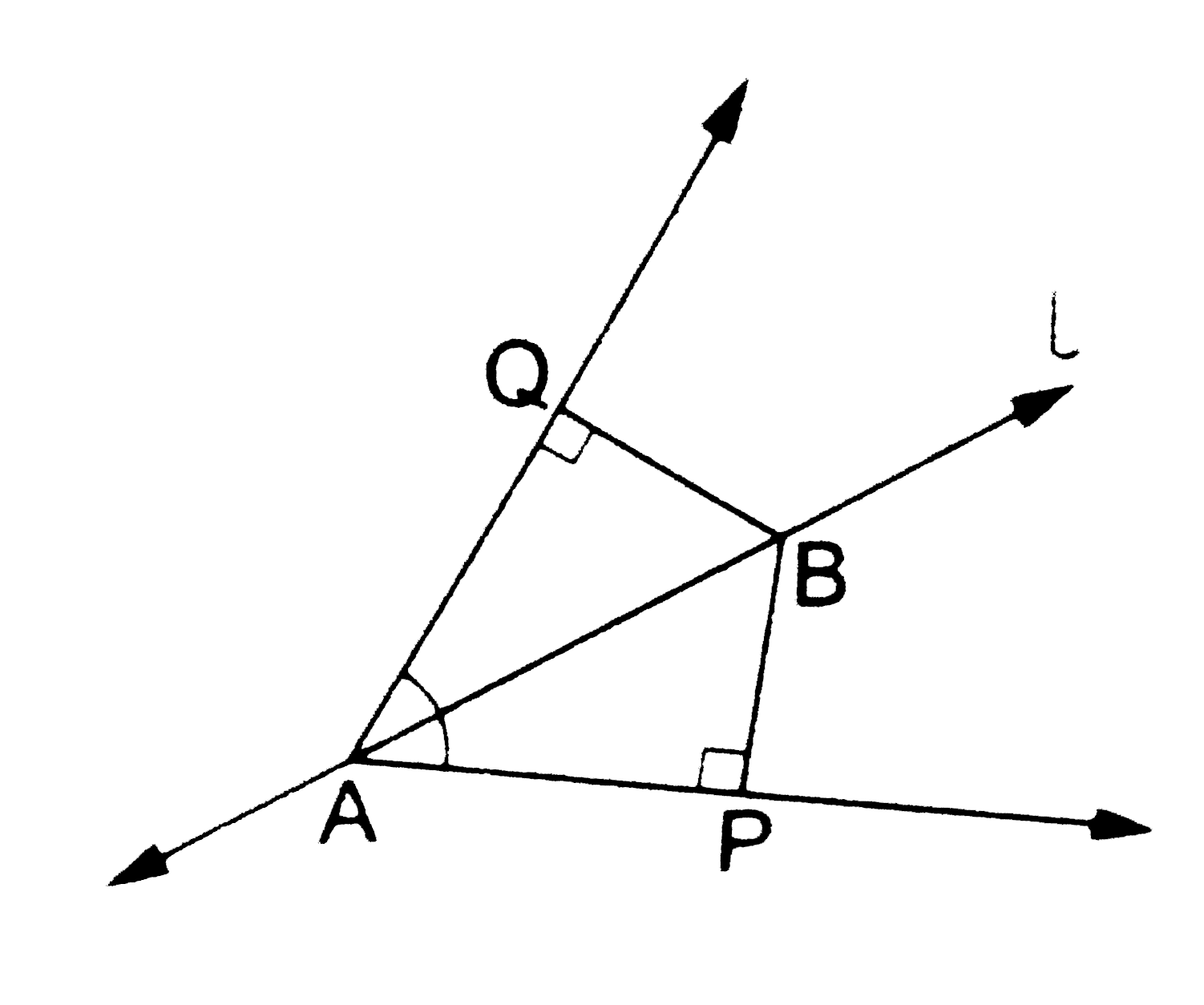
View SolutionIn the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
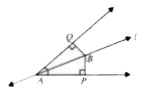
ΔAPB≅ΔAQB
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
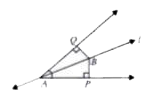
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionIn the given figure, line I is the bisector of an angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A. Show that B is equidistant from the arms of ∠A.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
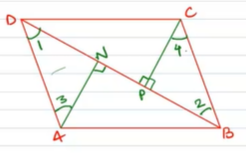
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View Solution
