Let ABCD be rectangle and Let E & F be points on CD & BC respectively such that Area (ADE)=16, area (CEF)=9, and area (ABF)=25. the area of ADF=t, then [t15] is
Step by step video & image solution for Let ABCD be rectangle and Let E & F be points on CD & BC respectively such that Area (ADE) = 16, area (CEF) = 9, and area (ABF) = 25. the area of ADF=t, then [t/15] is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Let ABCD be a rectangle and let E and F be points on CD and BC respectively such that area (ADE)=16, area (CEF)=9 and area (ABF)=25 What si the area of triangle AEF?
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, ABCD is a rectangle. Points E and F cut the sides BC and CD of the rectangle respectively such that EC = 3, FC = 4, and AD = 12, and the area of the crossed and the shaded regions in the figure are equal. Which one of the following equals the perimeter of rectangle ABCD?
 A42B50C56D64
A42B50C56D64 - Question 2 - Select One
In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
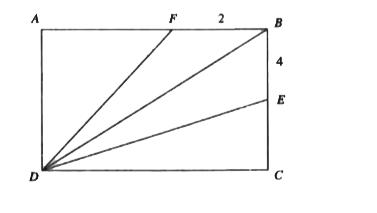 A18B23C30D42
A18B23C30D42 - Question 3 - Select One
If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
A13 are (ABCD)B34 area (ABCD)C12 area (ABCD)Darea (ABCD)
In a figure, ABCD is a rectangle and P & Q are mid-points of CD and BC respectively. Find ratio of area of shadow region and area of un-shad-owed region?
 View Solution
View SolutionLet P be an interior point of a convex quadrilateral ABCD and K, L, M, N be the midpoints of AB, BC, CD, DA respectively. If Area(PKAN)=25, Area(PLBK)=36, and Area(PMDN)=41 then Area(PLCM) is
View SolutionIn a triangle ABC, D and E are points on AB, AC respectively such that DE is parallel to BC. Suppose BE, CD intersect at O. If the areas of the triangles ADE and ODE are 3 and 1 respectively, find the area of the triangle ABC, with justification
View SolutionLet ABC be a triangle such that AB = 4, BC = 5 and CA = 6. Choose points D,E,F on AB, BC, CA respectively, such that AD = 2, BE = 3, CF=4. Then areaΔDEFareaΔABC is
View SolutionIn the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
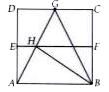 View Solution
View Solution

