Let P be an interior point of a convex quadrilateral ABCD and K, L, M, N be the midpoints of AB, BC, CD, DA respectively. If Area(PKAN)=25, Area(PLBK)=36, and Area(PMDN)=41 then Area(PLCM) is
20
29
52
54
To find the area of the quadrilateral PLCM given the areas of the other quadrilaterals, we can follow these steps:
1. Identify the Areas:
- We are given:
- Area(PKAN) = 25
- Area(PLBK) = 36
- Area(PMDN) = 41
- We need to find Area(PLCM).
2. Assign Variables:
- Let:
- Area(PKAN) = x + z = 25
- Area(PLBK) = x + y = 36
- Area(PMDN) = w + z = 41
- Here, x, y, w, and z represent the areas of the smaller triangles formed by point P and the midpoints K, L, M, N.
3. Set Up Equations:
- From the areas, we can set up the following equations:
1. x+z=25 (Equation 1)
2. x+y=36 (Equation 2)
3. w+z=41 (Equation 3)
4. Combine Equations:
- Add Equation 2 and Equation 3:
(x+y)+(w+z)=36+41
This simplifies to:
x+y+w+z=77(Equation4)
5. Subtract Equation 1 from Equation 4:
- Now, subtract Equation 1 from Equation 4:
(x+y+w+z)−(x+z)=77−25
This simplifies to:
y+w=52
6. Conclusion:
- Since Area(PLCM) = y + w, we find that:
Area(PLCM)=52
Final Answer:
The area of quadrilateral PLCM is 52.
- We are given:
- Area(PKAN) = 25
- Area(PLBK) = 36
- Area(PMDN) = 41
- We need to find Area(PLCM).
- Let:
- Area(PKAN) = x + z = 25
- Area(PLBK) = x + y = 36
- Area(PMDN) = w + z = 41
- Here, x, y, w, and z represent the areas of the smaller triangles formed by point P and the midpoints K, L, M, N.
- From the areas, we can set up the following equations:
1. x+z=25 (Equation 1)
2. x+y=36 (Equation 2)
3. w+z=41 (Equation 3)
- Add Equation 2 and Equation 3:
(x+y)+(w+z)=36+41
This simplifies to:
x+y+w+z=77(Equation4)
- Now, subtract Equation 1 from Equation 4:
(x+y+w+z)−(x+z)=77−25
This simplifies to:
y+w=52
- Since Area(PLCM) = y + w, we find that:
Area(PLCM)=52
The area of quadrilateral PLCM is 52.
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
A13 are (ABCD)B34 area (ABCD)C12 area (ABCD)Darea (ABCD) - Question 2 - Select One
Consider a square ABCD of side 12 and let M, N be the midpoints of AB, CD respectively. Take a point P on MN and let AP=r, PC=s. Then the area of the triangle whose sides are r, s, 12 is-
A72B36Crs2Drs7
Area of square ABCD is 4 unit2.MandN are mid points of ABandBC. Find PC.
View SolutionABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionLet ABCD be rectangle and Let E & F be points on CD & BC respectively such that Area (ADE)=16, area (CEF)=9, and area (ABF)=25. the area of ADF=t, then [t15] is
View SolutionIn the given figure, ABCD is a rectangle in which AB = 40 cm and BC = 25 cm. If P. Q, R, S be the midpoints of AB, BC, CD and DA respectively, find the area of the shaded region.
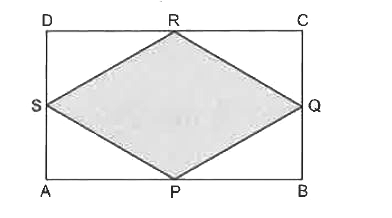 View Solution
View SolutionLet ABCD be a rectangle and let E and F be points on CD and BC respectively such that area (ADE)=16, area (CEF)=9 and area (ABF)=25 What si the area of triangle AEF?
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
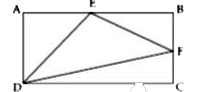 View Solution
View Solution

