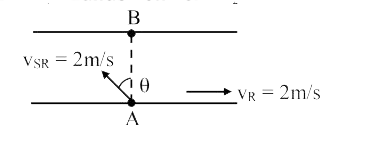
Find θ in the given situation so that the swimmer directly lands on the point B.
45∘
30∘
90∘
Not possible
The correct Answer is:d
For swimmer to land on the point B vSR>VR
since VSR=VR∴ Not possible
Similar Questions
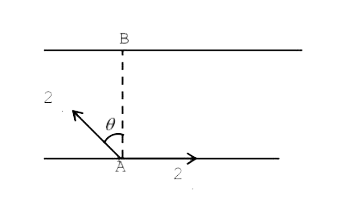
A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
 View Solution
View SolutionFor the given situation,the system is at rest,find the value of mass m :-
View Solution
Knowledge Check
- Question 1 - Select One
A person can swim in still water with speed =5km/hr. He enters a 200m. Wide river at a point A on one of the banks. The river flow velocity is uniform and equal to 6km/hr. A point B is located directly across. A, on the other bank. What is the closest possible distance from B where the swimmer can land on the other bank ?
A120mB40√11mC30√10mDNone of these - Question 2 - Select One
If speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
A127∘ with direction of river flowB60∘ with direction of river flowC143∘ with direction of river flowDSwimmer will never reach directly opposite end - Question 3 - Select One
A swimmer swims in still water at a speed =5km/hr. He enters a 200m wide river, having river flow speed =4km/hr at point A and proceeds to swim at an angle of 127∘(sin37∘=0.6) with the river flow direction. Another point B is located directly across A on the other side. the swimmer lands on the other bank at a point C, form which he walks the distance CB with a speed =3km/hr. The total time in which he reaches from A to B is
A5minutesB4minutesC3minutesDNone
Find the acceleration of the A and B in the situation show in the figure
 View Solution
View SolutionFind the equations of the tangent and the normal to the given curve at the indicated point :
x2a2−y2b2=1at'(asecθ,btanθ)View SolutionFind the equations of the tangent and the normal to the given curve at the indicated point :
x2a2+y2b2=1 at (acosθ,bsinθ)View SolutionIt is given that l varies directly as m.
Find m when l is 8.View SolutionIt is given that l varies directly as m.
Find l, when m is 33.View Solution

