A simple circuit contains an ideal battery and a resistance R. If a second resistor is placed in parallel with the first.
the potential across R will decrease
the current through R will decreased
the current delivered by the battery will increase
the power dissipated by R will increased.
The correct Answer is:C
To solve the problem of a simple circuit containing an ideal battery and a resistance R, with a second resistor placed in parallel with the first, we will analyze the effects of this configuration step by step.
Step 1: Understand the Circuit Configuration
In the original circuit, we have an ideal battery with an EMF (E) connected to a resistor R. When a second resistor (let's call it R2) is placed in parallel with R, we need to analyze how this affects the overall circuit.
Hint: Remember that resistors in parallel share the same voltage across them, which is equal to the EMF of the battery.
Step 2: Calculate the Equivalent Resistance
The equivalent resistance (R_eq) of two resistors in parallel (R and R2) can be calculated using the formula:
1Req=1R+1R2
This can be rearranged to find R_eq:
Req=R⋅R2R+R2
Hint: If R2 is equal to R, then the equivalent resistance becomes R/2.
Step 3: Analyze the Voltage Across Resistors
Since R and R2 are in parallel, the voltage across both resistors remains equal to the EMF of the battery (E). Thus, the voltage across R does not change.
Hint: The voltage across resistors in parallel is always the same and equal to the voltage of the source.
Step 4: Calculate the Current Through Each Resistor
Using Ohm's Law (V = IR), the current through resistor R (I_R) can be calculated as:
IR=ER
Similarly, the current through resistor R2 (I_R2) can be calculated as:
IR2=ER2
Hint: The total current supplied by the battery is the sum of the currents through each parallel resistor.
Step 5: Determine the Total Current from the Battery
The total current (I_total) delivered by the battery is the sum of the currents through R and R2:
Itotal=IR+IR2=ER+ER2
Hint: If R2 is equal to R, the total current will be double that of the current through a single resistor.
Step 6: Analyze the Power Dissipated by Resistor R
The power dissipated by resistor R (P_R) can be calculated using the formula:
PR=V2R=E2R
Since the voltage across R remains the same, the power dissipated does not change when R2 is added in parallel.
Hint: The power remains the same as long as the voltage across the resistor does not change.
Conclusion
1. The potential across R remains constant (equal to E).
2. The current through R does not decrease; it remains the same as before.
3. The total current delivered by the battery increases.
4. The power dissipated by R remains the same.
Final Answer
The correct statement is that the current delivery by the battery will increase.
In the original circuit, we have an ideal battery with an EMF (E) connected to a resistor R. When a second resistor (let's call it R2) is placed in parallel with R, we need to analyze how this affects the overall circuit.
The equivalent resistance (R_eq) of two resistors in parallel (R and R2) can be calculated using the formula:
1Req=1R+1R2
This can be rearranged to find R_eq:
Req=R⋅R2R+R2
Since R and R2 are in parallel, the voltage across both resistors remains equal to the EMF of the battery (E). Thus, the voltage across R does not change.
Using Ohm's Law (V = IR), the current through resistor R (I_R) can be calculated as:
IR=ER
Similarly, the current through resistor R2 (I_R2) can be calculated as:
IR2=ER2
The total current (I_total) delivered by the battery is the sum of the currents through R and R2:
Itotal=IR+IR2=ER+ER2
The power dissipated by resistor R (P_R) can be calculated using the formula:
PR=V2R=E2R
Since the voltage across R remains the same, the power dissipated does not change when R2 is added in parallel.
1. The potential across R remains constant (equal to E).
2. The current through R does not decrease; it remains the same as before.
3. The total current delivered by the battery increases.
4. The power dissipated by R remains the same.
The correct statement is that the current delivery by the battery will increase.
Similar Questions
Knowledge Check
Assertion : In the circuit shown in figure, battery is ideal. If a resistance R0 is cannected in parallel with R, then power across R will increase.
Reason : Current drawn from the battery will increase.AIf both Assertion and Reason are true and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are true and Reason is not correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.The effective resistance of a circuit containing resistances in parallel is
Aequal to the sum of the individual resistancesBsmaller than any of the individual resistancesCgreater than any of the individual resistancesDsometimes greater and sometimes smaller than the individual resistancesA simple circuit contains a 12 V battery and a bulb having 24 ohm resistance. When you turn on the switch, the ammeter connected in the circuit would read
A0.5AB2AC4AD5A
Two batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
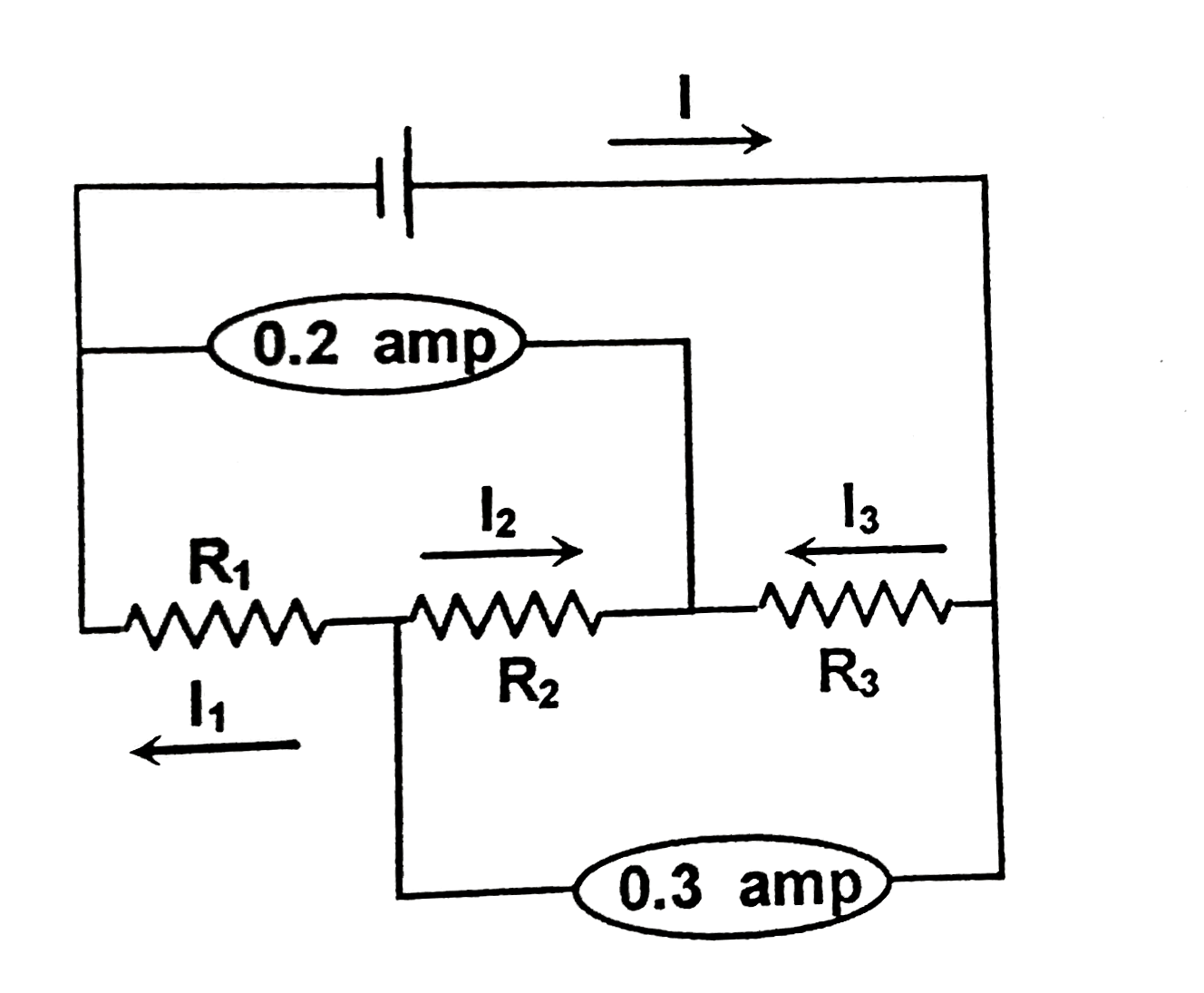
View SolutionA circuit contains an ideal battery, three resistors and two ideal ammeters. The ammeters read 0.2 amp and 0.3 amp. After two of the resistor are switched (inerchanged) the readings of ammeter do not change. Then
View SolutionCircuit A is made of resistors connected in series to a battery, circuit B is made of resistors connected in parallel to a battery. Let P be the power drawn from the batteries. As the number of resistors in each circuit is increased,
View SolutionA simple electric circuit has a 24V battery and a resistor of 60 ohms. What will be the current in the circuit? The resistance of the connecting wires is negligible.
View SolutionIn a circuit containing two unequal resistors connected in parallel :
View Solution
