Calculate the moment of intertia of an annular disc about an axis which lies in the plane of the disc and tangential to the inner circle. Mass of the disc is M and its inner radius is R1 and outer rad/R2.
To calculate the moment of inertia of an annular disc about an axis that lies in the plane of the disc and is tangential to the inner circle, we can follow these steps:
1. Understand the Geometry of the Annular Disc:
- The annular disc has an inner radius R1 and an outer radius R2.
- The axis we are interested in (let's call it axis AB) is tangential to the inner circle and lies in the plane of the disc.
2. Identify the Moment of Inertia about the Central Axis:
- The moment of inertia Iz of the annular disc about an axis perpendicular to the plane of the disc and passing through the center is given by:
Iz=M2(R21+R22)
3. Use the Perpendicular Axis Theorem:
- According to the Perpendicular Axis Theorem, for a planar body:
Iz=Ix+Iy
- Since the annular disc is symmetric, we have Ix=Iy. Therefore:
Iz=2Iy⟹Iy=Iz2=M4(R21+R22)
4. Apply the Parallel Axis Theorem:
- The axis AB is parallel to the y-axis (which we just calculated) and is at a distance R1 from it. The Parallel Axis Theorem states:
IAB=Iy+Md2
- Here, d is the distance between the two axes, which is R1. Thus:
IAB=Iy+MR21
5. Substitute the Values:
- Substitute Iy into the equation:
IAB=M4(R21+R22)+MR21
- Combine the terms:
IAB=M4(R21+R22)+4MR214=M4(R21+R22+4R21)
IAB=M4(5R21+R22)
6. Final Result:
- The moment of inertia of the annular disc about the axis AB is:
IAB=M4(5R21+R22)
- The annular disc has an inner radius R1 and an outer radius R2.
- The axis we are interested in (let's call it axis AB) is tangential to the inner circle and lies in the plane of the disc.
- The moment of inertia Iz of the annular disc about an axis perpendicular to the plane of the disc and passing through the center is given by:
Iz=M2(R21+R22)
- According to the Perpendicular Axis Theorem, for a planar body:
Iz=Ix+Iy
- Since the annular disc is symmetric, we have Ix=Iy. Therefore:
Iz=2Iy⟹Iy=Iz2=M4(R21+R22)
- The axis AB is parallel to the y-axis (which we just calculated) and is at a distance R1 from it. The Parallel Axis Theorem states:
IAB=Iy+Md2
- Here, d is the distance between the two axes, which is R1. Thus:
IAB=Iy+MR21
- Substitute Iy into the equation:
IAB=M4(R21+R22)+MR21
- Combine the terms:
IAB=M4(R21+R22)+4MR214=M4(R21+R22+4R21)
IAB=M4(5R21+R22)
- The moment of inertia of the annular disc about the axis AB is:
IAB=M4(5R21+R22)
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Calculate the moment of intertia of an annular disc about an axis which lies in the plane of the disc and tangential to the outer circle. Mass of the disc is M and its inner radius is R1 and outer rad/R2.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View Solution
Knowledge Check
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
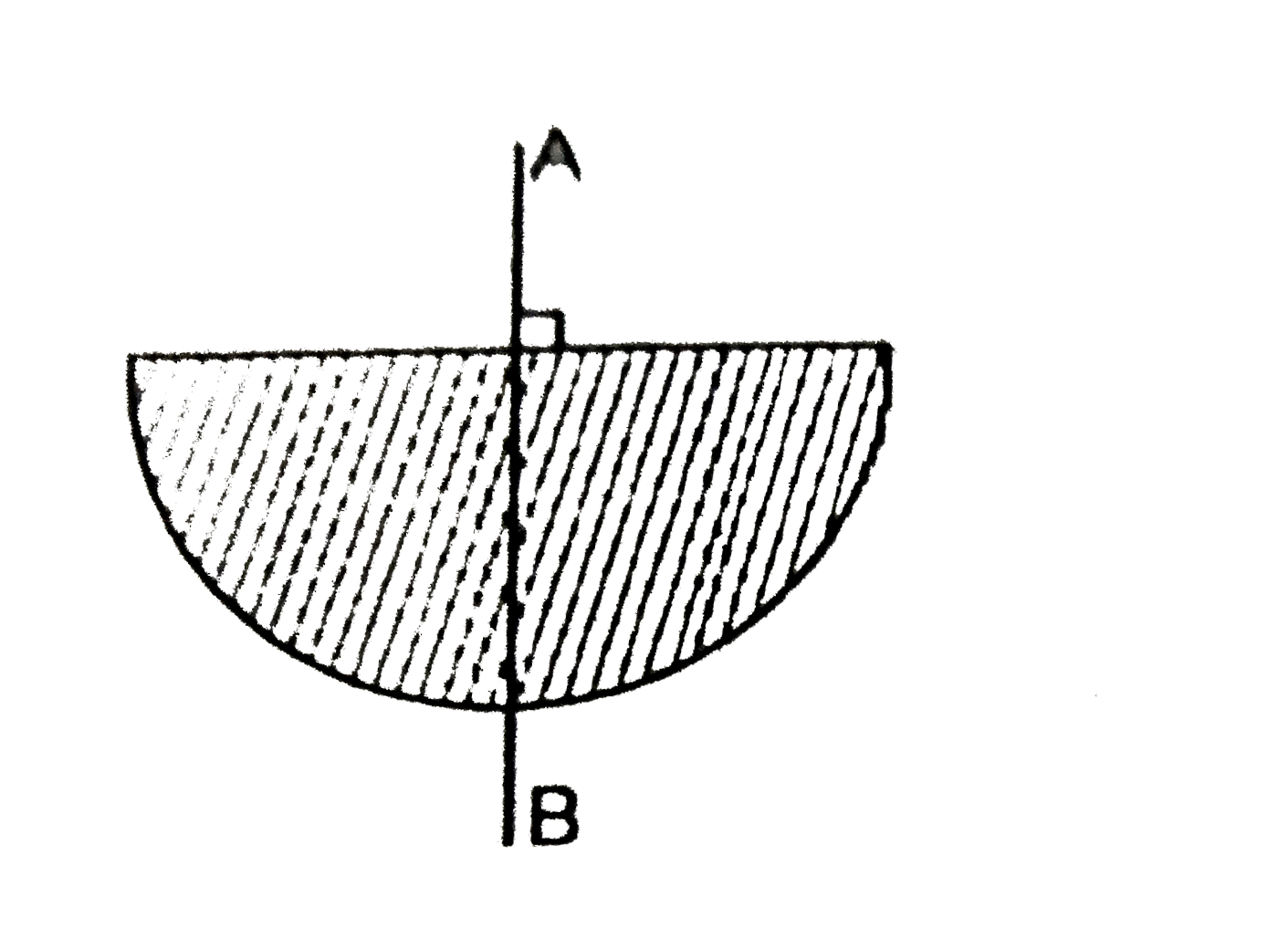 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2The moment of inertia of an annular disc of mass M, outer and inner radii R and r, about its diameter is
AM(R2+r2)/2BMR2CMr2DMR2+r24The moment of inertia of an annular disc of mass M, outer and inner radii R and r, about its diameter is
AM(R2+r2)/2BMR2CMr2DMR2+r24
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View Solution
