On meltng of ice on the pole of the earth, its moment of inertia will :-
increase
decrease
remain unchanged
none of these
The correct Answer is:A
To solve the problem regarding the moment of inertia of the Earth when ice melts at the poles, we can follow these steps:
1. Understanding Moment of Inertia:
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. It depends on the mass distribution relative to the axis of rotation. The formula for moment of inertia for point masses is given by:
I=∑mir2i
where mi is the mass of the particle and ri is the distance from the axis of rotation.
2. Effect of Melting Ice:
When ice at the poles melts, the water that results from the melting ice will flow towards the equator. This means that the mass of the Earth is redistributed from the poles (where the radius is smaller) to the equator (where the radius is larger).
3. Analyzing the Change in Radius:
The radius at the equator is greater than the radius at the poles. Since the moment of inertia is proportional to the square of the distance from the axis of rotation, moving mass from the poles to the equator increases the overall moment of inertia.
4. Mathematical Representation:
If we denote the mass of the ice that melts and moves to the equator as m, the moment of inertia contribution from the ice at the poles (with a smaller radius rp) will be:
Ipoles=mr2p
After melting, this mass contributes to the moment of inertia at the equator (with a larger radius re):
Iequator=mr2e
Since re>rp, it follows that:
Iequator>Ipoles
Thus, the total moment of inertia of the Earth increases.
5. Conclusion:
Therefore, when ice melts at the poles and moves to the equator, the moment of inertia of the Earth will increase.
Final Answer:
The moment of inertia of the Earth will increase when ice melts at the poles.
---
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. It depends on the mass distribution relative to the axis of rotation. The formula for moment of inertia for point masses is given by:
I=∑mir2i
where mi is the mass of the particle and ri is the distance from the axis of rotation.
When ice at the poles melts, the water that results from the melting ice will flow towards the equator. This means that the mass of the Earth is redistributed from the poles (where the radius is smaller) to the equator (where the radius is larger).
The radius at the equator is greater than the radius at the poles. Since the moment of inertia is proportional to the square of the distance from the axis of rotation, moving mass from the poles to the equator increases the overall moment of inertia.
If we denote the mass of the ice that melts and moves to the equator as m, the moment of inertia contribution from the ice at the poles (with a smaller radius rp) will be:
Ipoles=mr2p
After melting, this mass contributes to the moment of inertia at the equator (with a larger radius re):
Iequator=mr2e
Since re>rp, it follows that:
Iequator>Ipoles
Thus, the total moment of inertia of the Earth increases.
Therefore, when ice melts at the poles and moves to the equator, the moment of inertia of the Earth will increase.
The moment of inertia of the Earth will increase when ice melts at the poles.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-A )
46 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )
24 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Statement-1 : If earth shrink (without change in mass) to half of its present size, length of the day would become 6 hours.
Statement-2 : When the size of the earth will change, its moment of inertia will also change.
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View Solution
Knowledge Check
On account of melting of ice at the north pole, the moment of inertia of spinning earth
AincreasesBdecreasesCremains unchanged.Ddepends on the time.On account of melting of ice at the north pole the moment of inertia of spinning earth -
AincreasesBdecreasesCremains unchangedDdepends on the timeAssertion : If the ice on the polar caps of the earth melts, then length of day will increase.
Reason : Moment of inertia of the earth increases, as ice on polar caps melts.AIf both the Asseration and Reason are true and reason explains the Assertion :BIf both the Assertion and Reason are true but reason does ot explain the Assertion :CIf Assertion is true but reason falseDIf Assertion is false but reason is true
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionThe position of axis of rotation of a body is changed so that its moment of inertia decreases so that its moment of inertia decreases by 36%. The % change in its radius of gyration is
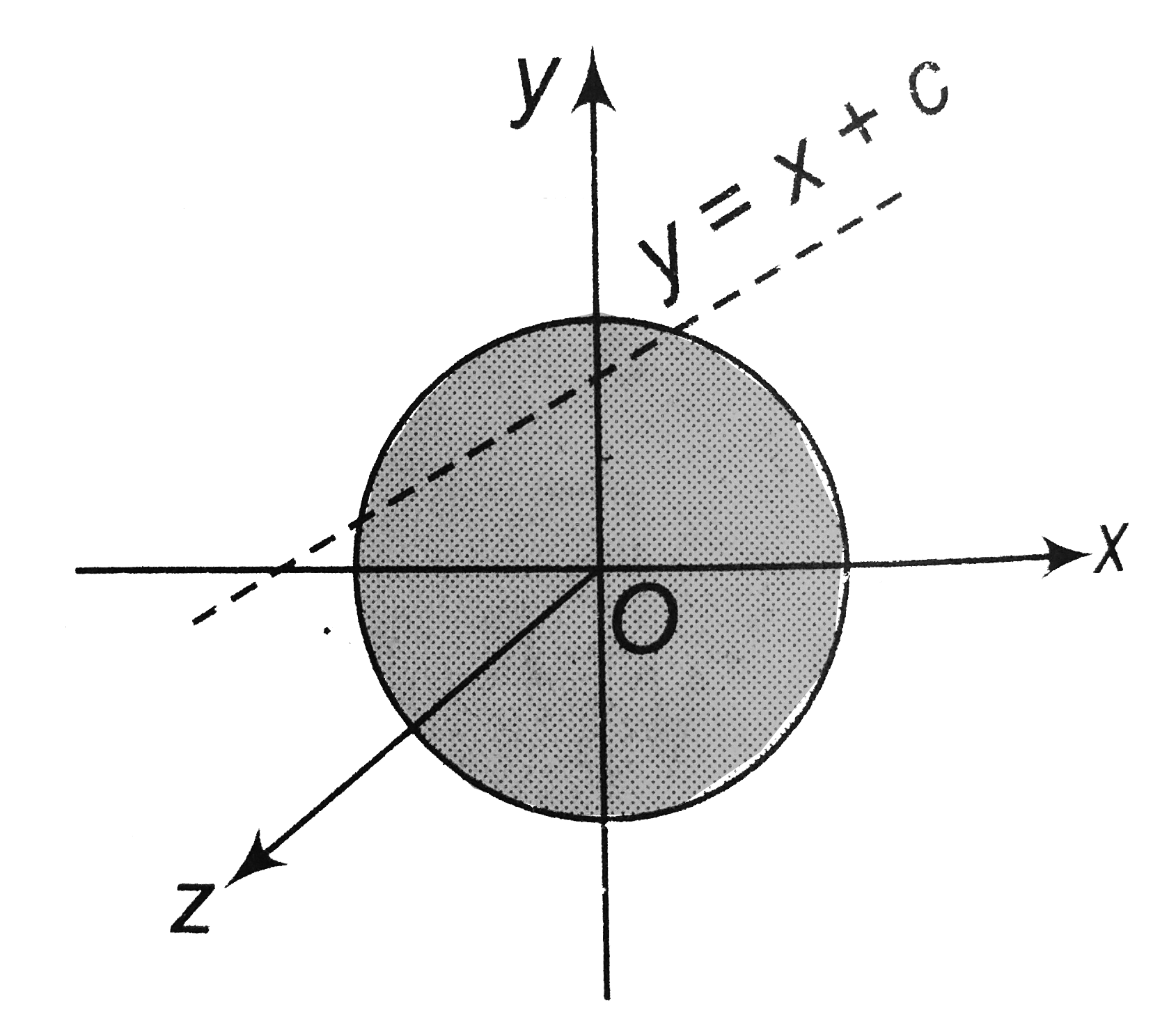
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .
.
View SolutionAssertion : If ice on the pole melts, length of the day will shorten.
Reason: Ice will flow towards equator and will result in the decrease in moment of inertia of earth resulting in decrease in frequency of rotation of earth.
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View Solution
