समलम्ब चतुर्भुज ABCD में AB||DC है। AD व BC पर कर्मश: E और F इस प्रकार स्थित है की EF∣∣AB है। सिद्ध कीजिए| AEED=BFFC.
Step by step video & image solution for समलम्ब चतुर्भुज ABCD में AB||DC है। AD व BC पर कर्मश: E और F इस प्रकार स्थित है की EF||AB है। सिद्ध कीजिए| (AE)/(ED)=(BF)/(FC). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समरूपता BOOK - SANJEEV PUBLICATIONCHAPTER - समरूपता EXERCISE - अन्य महत्वपूर्ण प्रश्न (निबंधात्मकप्रश्न)
5 Videos
- समरूपता BOOK - SANJEEV PUBLICATIONCHAPTER - समरूपता EXERCISE - अन्य महत्वपूर्ण प्रश्न (अतिलघुत्तरात्मक प्रश्न)
13 Videos
- वैदिक गणित BOOK - SANJEEV PUBLICATIONCHAPTER - वैदिक गणित EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुत्तरात्मक प्रश्न)
13 Videos
- समान्तर श्रेढ़ीBOOK - SANJEEV PUBLICATIONCHAPTER - समान्तर श्रेढ़ीEXERCISE - (अन्य महत्त्वपूर्ण प्रश्न) निबन्धात्मक प्रश्न
2 Videos
Similar Questions
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है कि AOBO=CODO है सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है।
View Solution△ABC में AD कोण BAC का समद्विभाजक है। यदि AB=4 cm, AC=6 cm, BD=2 cm है तो BC का मान ज्ञात कीजिए।
View Solutionयोग ज्ञात कीजिए (शून्यान्त संख्या विधि)
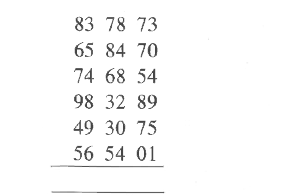
View Solutionयदि किसी समान्तर श्रेढ़ी के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो उसके प्रथम पदों का योग ज्ञात कीजिए।
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD एक समलम्ब हैं जिसमे AB ||DC हैं । असमान्तर भुजाओं AD और BC पर क्रमशः बिन्दु E और F इस प्रकार स्थित हैं कि EF भुजा AB के समान्तर हैं दर्शाइए कि AEED=EFFC हैं ।
View SolutionABCD एक समलम्ब चतुर्भुज है । जहा AB।।DC बिन्दु E तथा F, क्रमशः असमान्तर भुजाओं AD तथा BC पर है तथा EF, AB के समान्तर है । तो सिद्ध कीजिए कि
AEED=BFFC
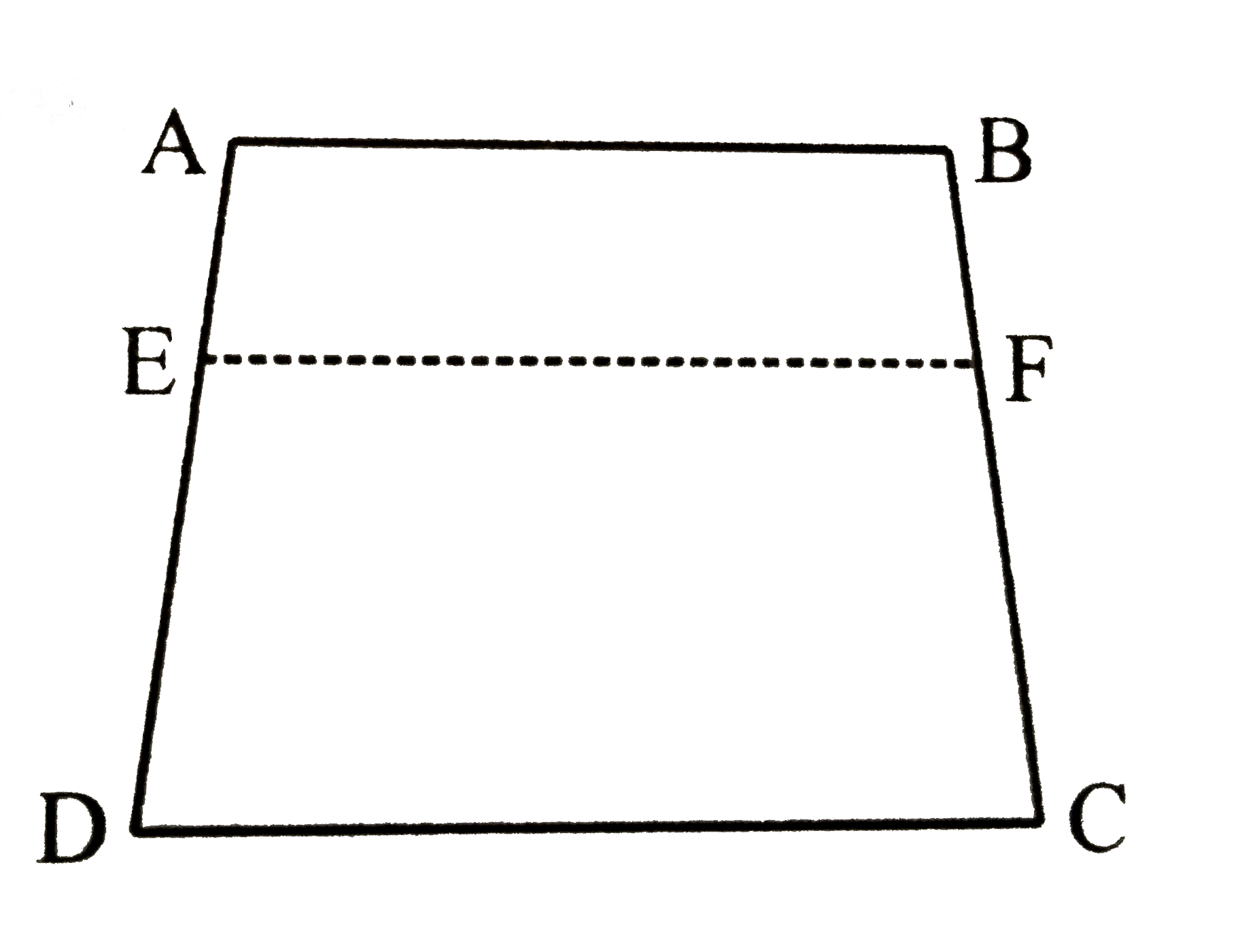
View SolutionABCD एक समचतुर्भुज है। AB को E व F की ओर इस प्रकार बढ़ाया जाता है AE=AB=BF
सिद्ध कीजिए की ED व FC परस्पर लम्ब है।
View Solutionचित्र में यदि EF||DC||AB हो, तो सिद्ध कीजिए की: AEED=BFFC
View SolutionIn trapezlum ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that AEED=BFFC.
View SolutionIn trapezium ABCD, AB∣∣DC. E and F are points on non-parallel sides AD and BC respectively such that EF∣∣AB.
Show that AEED=BFFC.
View Solutionசரிவகம் ABCD -யில் ,AB ||DC ,E மற்றும் F என்பன முறையே இணையற்ற பக்கங்கள் AD மற்றும் BC -யின் மீது அமைந்துள்ள புள்ளிகள் ,மேலும் EF ||AB என அமைந்தால் ,AEED =BFFC என நிறுவுக ?
View SolutionIn trapezium ABCD, AB∣∣DC. E and F are points on non-parallel sides AD and BC respectively such that EF∣∣AB.
Show that AEED=BFFC.
View SolutionIn trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View SolutionIn trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View Solution