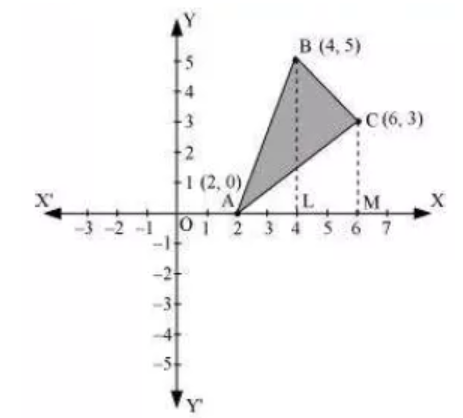
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).

Video Solution

Text Solution

Verified by Experts

Equation of line joining A and B is $\frac{y - 0}{x - 2} = \frac{5 - 0}{4 - 2} \Rightarrow y = \frac{5 x}{2} - 5$
Equation of line joining B and C is $\frac{y - 5}{x - 4} = \frac{5 - 3}{4 - 6} \Rightarrow y = 9 - x$
Equation of line joining A and C is $\frac{y - 0}{x - 2} = \frac{3 - 0}{6 - 2} \Rightarrow y = \frac{3 x}{4} - \frac{3}{2}$
ar(ABC)=ar(ABL)+ar(LBCM)-ar(ACM)
Now
ar(ABL)= $\int_{2}^{4} (\frac{5 x}{2} - 5) d x = {[\frac{5 x^{2}}{4} - 5 x]}_{2}^{4} = (20 - 20) - (5 - 10) = 5$ units
ar(LBCM)= $\int_{4}^{6} (9 - x) d x = {[9 x - \frac{x^{2}}{2}]}_{4}^{6} = (54 - 18) - (36 - 8) = 8$ units
ar(ACM) = $\int_{2}^{6} (\frac{3 x}{4} - \frac{3}{2}) d x = {[\frac{3 x^{2}}{8} - \frac{3 x}{2}]}_{2}^{6} = (\frac{27}{2} - 9) - (\frac{3}{2} - 3) = 6$ units
Hence
ar(ABC) = $8 + 5 - 6 = 7$ units

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT-APPLICATION OF INTEGRALS-MISCELLANEOUS EXERCISE

Home
Ask Doubt
Profile