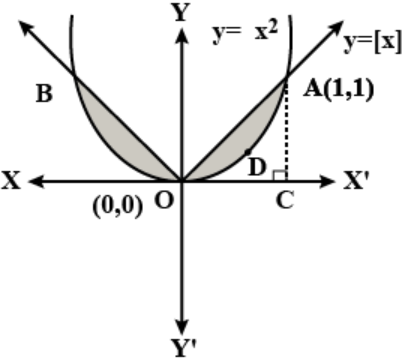
Find the area bounded by curves ${(x, y) : y \geq x^{2} and y = | x |}$

Video Solution

Text Solution

Verified by Experts

The given curve is ${(x, y) : y \geq x^{2} and y = | x |}$
shaded region is
It can be observed that the required area is symmetrical about y-axis.
Required area = $2 [A r e a (O C A O) - A r e a (O C A D O)]$
$= 2 [\int_{0}^{1} x d x - \int_{0}^{1} (x^{2}) d x]$
= $2 [{(\frac{x^{2}}{2})}_{0}^{1} - {(\frac{x^{3}}{3})}_{0}^{1}]$
= $2 [\frac{1}{2} - \frac{1}{3}]$ = $2 [\frac{1}{6}]$ = $\frac{1}{3}$ sq. units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these

NCERT-APPLICATION OF INTEGRALS-MISCELLANEOUS EXERCISE

Home
Ask Doubt
Profile