15.40 में दिए गए दो आरेख दो वर्तुल गतियों के तदनुरूपी हैं | प्रत्येक आरेख पर वृत्त की त्रिज्या, परिक्रमण - काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शायी गयी है | प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्या- सदिश के x - अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति का समीकरण ज्ञात कीजिए |
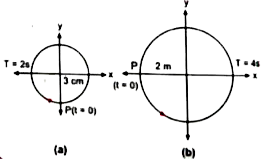
चित्र 15.41 (a) में, कण p दक्षिणावर्त परिक्रम करना शुरू करता है, यदि यह t समय बाद बिंदु Q पर पहुँचता है
तो कोण
θ=ωt=2πtT,(∴T=2) सेकंड
θ=2πr2=πt रेडियन
कण का विस्थापन =ON
= OQcos(π2−θ)=OQsinθ
ON=-x सेमी (जो मूल बिंदु से बायीं और है)
−x=OQsinθ
प्रश्नानुसार, OQ = 3 सेमी, तथा θ=πt, से,
x=−3sinπt
यह समीकरण कण की सरल आवर्त गति का आवश्यक समीकरण है|
चित्र में , कण वामावर्त परिक्रम करना शुरू करता है, यदि वह t समय में बिंदु Q तक पहुँचता है तो कोण θ=ωt=2πtT,θ=2πt4=πt2(∴T=4) सेकंड
कण का विस्थापन =ON = OQcosθ
माना ON=-x cm है, OQ =2 मीटर (दिया है)
−x=2cosθ
x=−2cos(πt)2 meter
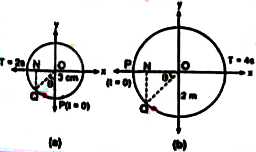
यह समीकरण कण की सरल आवर्त गति का आवश्यक समीकरण है|
Topper's Solved these Questions
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - वस्तुनिष्ठ प्रश्न
79 Videos
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - संख्यात्मक प्रश्न
22 Videos
- तरल के यान्त्रिक गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - वस्तुनिष्ठ प्रश्न
70 Videos
- द्रव्य के तापीय गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - वस्तुनिष्ठ प्रश्न
180 Videos
Similar Questions
सरल आवर्त गति करते हुए एक कण के सम्बन्ध में असत्य कथन है :
View Solutionसरल आवर्त गति करते हुए कण का आवर्तकाल 0.5 सेकण्ड तथा आयाम 10 सेमी है | कण का अधिकतम वेग ज्ञात कीजिए |
View Solutionगलत कथन है :
View Solutionसेल्सियस स्केल पर परम शून्य की माप −273.15∘C है। फारेनहाइट स्केल पर परम शून्य की माप होगी :
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionकाव्यांश के आधार पर परशुराम के स्वभाव की दो विशेषताओं पर सोदाहरण टिप्पणी कीजिए।
View Solutionगुरुत्वाकर्षण|उपग्रह का परिक्रमण काल #!#उपग्रह की कुल ऊर्जा
View Solution"बेटी की आँखें मंदिर में दीवट पर जलते घी के दो दिए है" में कौन-सा अलंकार है?
View Solutionएक बिंदु की शक्ति | किसी अन्य वृत्त के सापेक्ष दिए गए वृत्त की स्थिति
View SolutionIn a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is: एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionIn a circle, two equal and parallel chords are 6 cm apart and they lie on the opposite sides of the centre of the circle, whose radius is 5 cm. The length of each chord (in cm), is एक वृत्त में, दो समान और समानान्तर जीवा 6 सेमी के दुरी पर हैं और वे वृत्त के केंद्र के विपरीत किनारों पर स्थित हैं, जिसकी त्रिज्या 5 सेमी है। प्रत्येक जीवा की लंबाई (सेमी में ) है:
View SolutionIf the angle between two radii of a circle be 130^@ , then the angle between the tangents at the end of these radii is: यदि किसी वृत्त की दो त्रिज्या के बीच का कोण 130^@ है, तो इन त्रिज्या के अंत में स्पर्शरेखाओं के बीच का कोण है
View Solutionसमान परास के दो प्रक्षेप्यो की तुलना |प्रक्षेप पथ का समीकरण|प्रक्षेपण पर महत्वपूर्ण उदाहरण|OMR|Summary
View Solution
