Question

Find the area of the region bounded by the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Explanation

To find the area of the region bounded by the ellipse given by the equation:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

we can follow these steps:

Step 1: Understand the Geometry of the Ellipse
The ellipse is symmetric about both the x-axis and the y-axis. The points where the ellipse intersects the axes are:
- On the x-axis: (a, 0) and (-a, 0)
- On the y-axis: (0, b) and (0, -b)

Step 2: Divide the Area into Quadrants
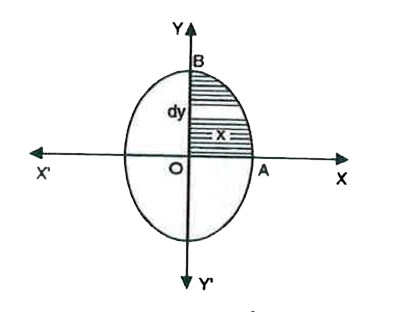
Due to the symmetry of the ellipse, we can calculate the area in one quadrant and then multiply it by 4 to get the total area. We will focus on the first quadrant where \(x \geq 0\) and \(y \geq 0\).

Step 3: Set Up the Integral for Area in the First Quadrant
In the first quadrant, we can express \(y\) in terms of \(x\) using the ellipse equation. Rearranging the equation gives:

\( y = b \sqrt{1 - \frac{x^2}{a^2}} \)

The area \(A_1\) in the first quadrant can be calculated using the integral:

\( A_1 = \int_0^a y \, dx = \int_0^a b \sqrt{1 - \frac{x^2}{a^2}} \, dx \)

Step 4: Simplify the Integral
We can factor out the constant \(b\):

\( A_1 = b \int_0^a \sqrt{1 - \frac{x^2}{a^2}} \, dx \)

Step 5: Use a Substitution
Let \(x = a \sin(\theta)\), then \(dx = a \cos(\theta) d\theta\). The limits change as follows:
- When \(x = 0\), \(\theta = 0\)
- When \(x = a\), \(\theta = \frac{\pi}{2}\)

Substituting into the integral gives:

\( A_1 = b \int_0^{\frac{\pi}{2}} \sqrt{1 - \sin^2(\theta)} \cdot a \cos(\theta) \, d\theta \)

Since \(\sqrt{1 - \sin^2(\theta)} = \cos(\theta)\), we have:

\( A_1 = b \int_0^{\frac{\pi}{2}} a \cos^2(\theta) \, d\theta \)

Step 6: Evaluate the Integral
Using the identity \(\cos^2(\theta) = \frac{1 + \cos(2\theta)}{2}\):

\( A_1 = \frac{ab}{2} \int_0^{\frac{\pi}{2}} (1 + \cos(2\theta)) \, d\theta \)

Calculating the integral:

\( \int_0^{\frac{\pi}{2}} 1 \, d\theta = \frac{\pi}{2}, \quad \int_0^{\frac{\pi}{2}} \cos(2\theta) \, d\theta = 0 \)

Thus:

\( A_1 = \frac{ab}{2} \cdot \frac{\pi}{2} = \frac{\pi ab}{4} \)

Step 7: Calculate the Total Area
Since the total area \(A\) of the ellipse is four times the area of the first quadrant:

\( A = 4A_1 = 4 \cdot \frac{\pi ab}{4} = \pi ab \)

Final Result
The area of the region bounded by the ellipse is:

\( \boxed{\pi ab} \)