किसी त्रिभुज ΔABC में, ∠B=60∘ , ∠C=40∘ है यदि AD तथा AE क्रमश: ∠A के आतंरिक समद्विभाजक तथा BC पर लंबवत है| ∠DAE ज्ञात करे?
5∘
10∘
40∘
60∘
The correct Answer is:B
According to question,

Given: ∠B=60∘
∠C=40∘
As we know that
∠A+∠B+∠C=180∘
∠A=180∘−60∘−40∘
As we know at
∠A+∠B+∠C=180∘
∠A=180∘−60∘−40∘
∴∠BAD=80∘2=40∘
In ΔAEB
∠A+∠B+∠E=180∘
∠A=180∘−60∘−90∘
∠A=30∘
Then, ∠DAE=∠DAB=∠EAB
40−30
∠DAE=10∘
By trick:
∠DAC=∠B−∠C2
=60∘−40∘2=10∘
Topper's Solved these Questions
Similar Questions
1,00,000 की राशि पर दो तरह के बट्टे, जिसमे एक बट्टा 40% है और दूसरा बट्टा दो क्रमवार 36% तथा 4% है दोनों तरह के बट्टे में कितना अंतर है
02:20View Solutionज़मींन पर किसी बिंदु से एक विमान उन्नतांश 45∘ है । 15 सेकेण्ड उड़ने के बाद उन्नतांश घटकर 30∘ हो जाता है । यदि विमान 2500 मीटर की ऊंचाई पर उड़ रहा है , तो विमान की गति कितने की . मि. /घंटा है ?
02:58View Solution△ABC में ∠B=70∘, और ∠C=30∘ , AD और AE क्रमश: भुजा BC पर लंब और ∠A की समद्विभाजक है । ∠DAE की माप कितनी है ?
03:17View SolutionΔABC में ∠B=35∘,∠C=65∘ तथा AD,∠BAC का समद्विभाजक BC से D पर मिलता है । तब निम्न में से कौन - सा सत्य है ?
 07:05View Solution
07:05View Solutionसंलग्न चित्र में, ΔABC में, ∠B=30∘, ∠C=65∘ तथा ∠A का समद्विभाजक BC पर X में मिलता है। दिखाइये कि CX<AX<BX
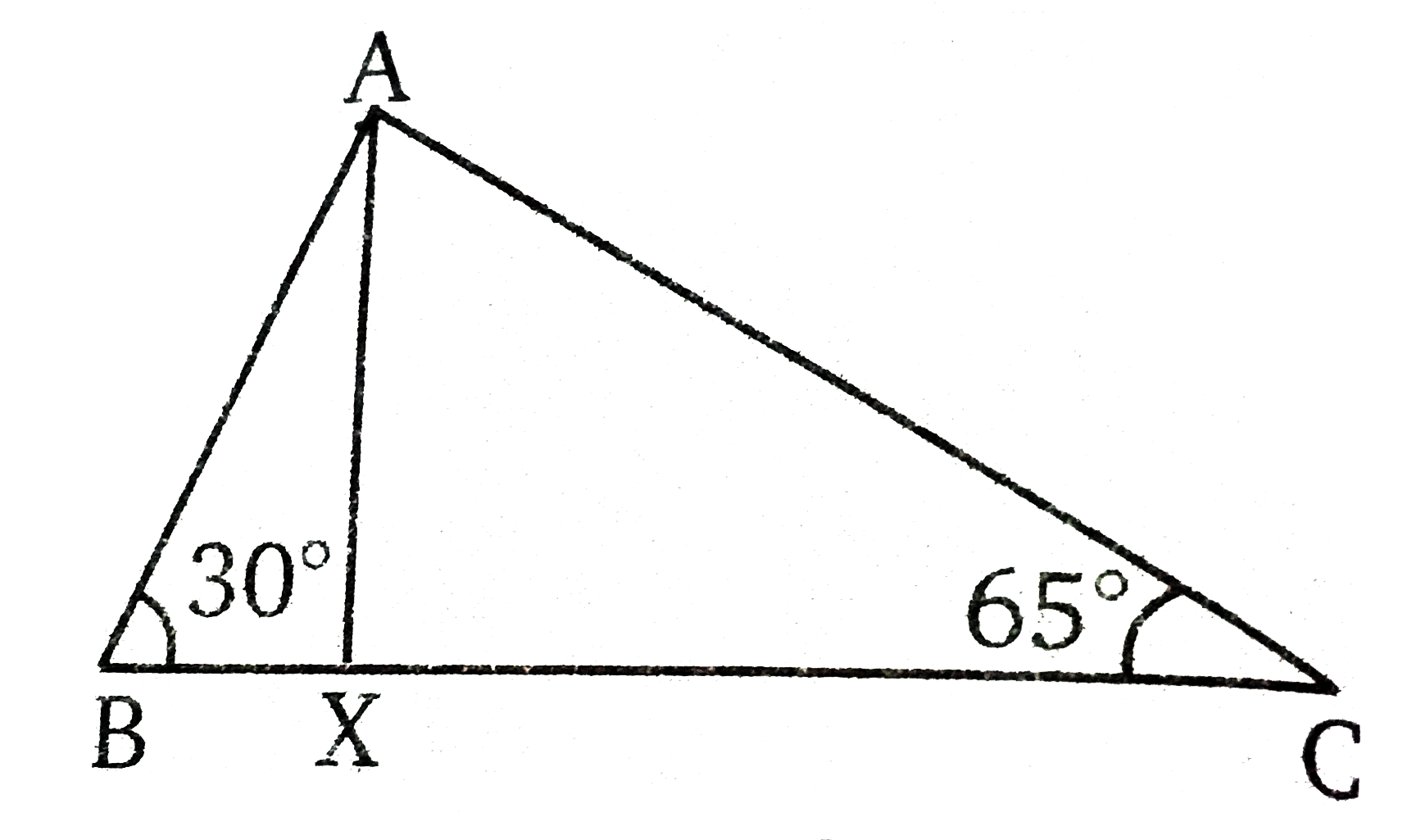 06:09View Solution
06:09View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
07:31View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
01:19View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
05:04View SolutionIn ΔABC, AB=BC=AC then ∠A=∠B=∠C=…….
14:32View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।
 05:44View Solution
05:44View Solutionसमाकलन के द्वारा त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षो A, B तथा C के निर्देशांक क्रमश : (2,3), (4,7) तथा (6,2) है।
03:43View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
03:22View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
03:52View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
05:00View SolutionIn triangle ABC ,D and E are the points on sides AC and AB, respectively, such that angle ADE= angle B . If AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then DE is equal to: त्रिभुज ABC में, D तथा E भुजा AC और AB पर स्थित ऐसे बिंदु angle ADE= angle B है| यदि AD =7.6 सेमी, AE = 7.2 सेमी, BE = 4.2 सेमी तथा BC = 8.4 सेमी है, तो DE किसके बराबर है ?
06:37View Solution

