A projectile is projected with a velocity u at an angle θ with the horizontal. For a fixed θ, which of the graphs shown in the following figure shows the variation of range R versus u?
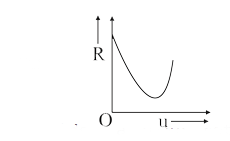

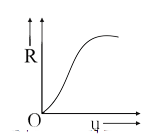
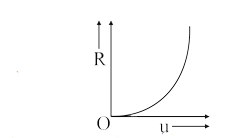
The correct Answer is:D
To solve the problem of determining the variation of range R versus initial velocity u for a projectile launched at a fixed angle θ, we can follow these steps:
1. Understanding the Range Formula:
The range R of a projectile launched with an initial velocity u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
2. Identifying Fixed Parameters:
In this scenario, the angle θ is fixed. This means that sin(2θ) is a constant value for a given θ. Therefore, we can denote this constant as k=sin(2θ).
3. Rewriting the Range Formula:
Substituting k into the range formula, we get:
R=u2kg
This shows that the range R is directly proportional to the square of the initial velocity u.
4. Establishing the Relationship:
Since R is proportional to u2, we can express this relationship as:
R∝u2
This indicates that as u increases, R increases with the square of u.
5. Graphical Representation:
The relationship R∝u2 suggests that if we plot R on the y-axis and u on the x-axis, the graph will be a parabola opening upwards. The general form of the equation for such a graph is:
R=k′u2
where k′ is a constant.
6. Identifying the Correct Graph:
Among the options provided, the graph that represents a quadratic relationship (a parabola) is the one that shows R increasing as u2. Therefore, the correct option is the one that resembles the shape of a parabola.
Conclusion:
The graph that shows the variation of range R versus initial velocity u is a parabola, confirming that R is proportional to u2.
The range R of a projectile launched with an initial velocity u at an angle θ is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity.
In this scenario, the angle θ is fixed. This means that sin(2θ) is a constant value for a given θ. Therefore, we can denote this constant as k=sin(2θ).
Substituting k into the range formula, we get:
R=u2kg
This shows that the range R is directly proportional to the square of the initial velocity u.
Since R is proportional to u2, we can express this relationship as:
R∝u2
This indicates that as u increases, R increases with the square of u.
The relationship R∝u2 suggests that if we plot R on the y-axis and u on the x-axis, the graph will be a parabola opening upwards. The general form of the equation for such a graph is:
R=k′u2
where k′ is a constant.
Among the options provided, the graph that represents a quadratic relationship (a parabola) is the one that shows R increasing as u2. Therefore, the correct option is the one that resembles the shape of a parabola.
The graph that shows the variation of range R versus initial velocity u is a parabola, confirming that R is proportional to u2.
Similar Questions
Knowledge Check
A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
A(a) Varies linearly with timeB(b) Is constant throughoutC(c) Is negative for complete pathD(d) None of the aboveA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
 Ais zero when particle is at the originBis −mv3sin2θcosθ2gˆk when particle is at the highest point of trajectoryCis −2mv2sin2θcosθgˆk when particle is just about to hit groundDdownward force of gravity exerts a torque in −z direction.
Ais zero when particle is at the originBis −mv3sin2θcosθ2gˆk when particle is at the highest point of trajectoryCis −2mv2sin2θcosθgˆk when particle is just about to hit groundDdownward force of gravity exerts a torque in −z direction.A projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
Aucosθ2BucosθCu(2cos(θ)2−sec(θ)2)Du(cos(θ)2−sec(θ)2)
A projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionA projectile is fired with a velocity 'u' making an angle θ with the horizontal. Show that its trajectory is a parabola.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
View SolutionA projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View Solution

