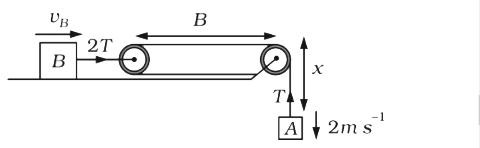
The velocity of the block B is:

2ms−1
3ms−1
1ms−1
6ms−1
The correct Answer is:C
x + 2y = L (length of string)
dxdt+2dydt=0⇒−dydt=12(dxdt)vB=12(2)=1ms−1
Applying tension trick,
2T(VB)−T(2)=0⇒2T(VB)=2T∴VB=1ms−1
Similar Questions
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

View Solution
Knowledge Check
A 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
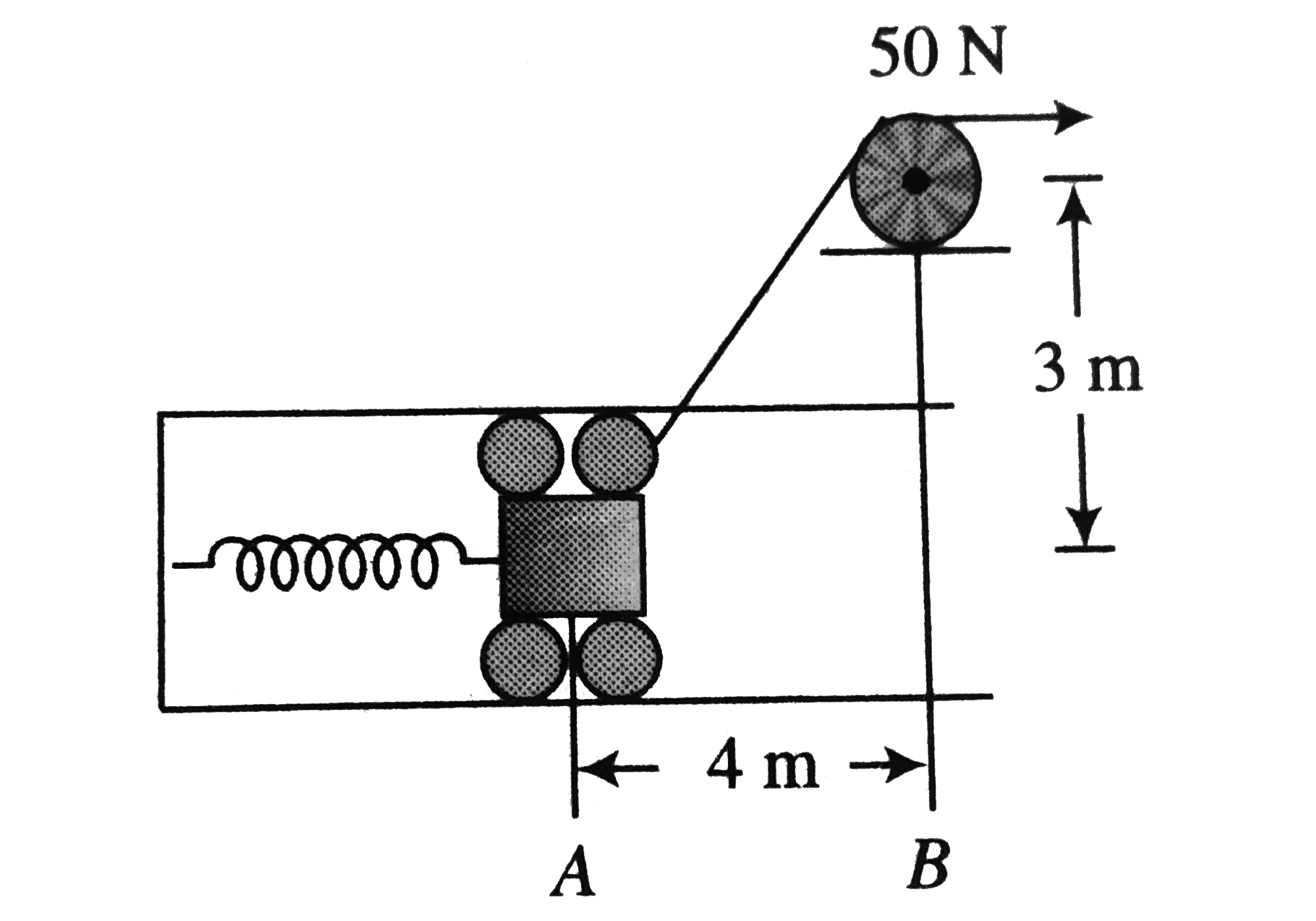 A(a) 4ms−1B(b) 2ms−1C(c) 1ms−1D(d) 3ms−1
A(a) 4ms−1B(b) 2ms−1C(c) 1ms−1D(d) 3ms−1Rod AO3 of length L can rotate abput A. Initially rod was at position AO2, when spring OB of force constant K, attached to block B of mass m was at position OA with unstretched length L. The smooth block B can slide on rod when pulled by the block D of mass m through a massless spring and smooth pulley at O1.
Find the velocity of the block B, when the rod and spring at B make an angle of 30∘ with their respective initial positions : (B is the middle point of the block)
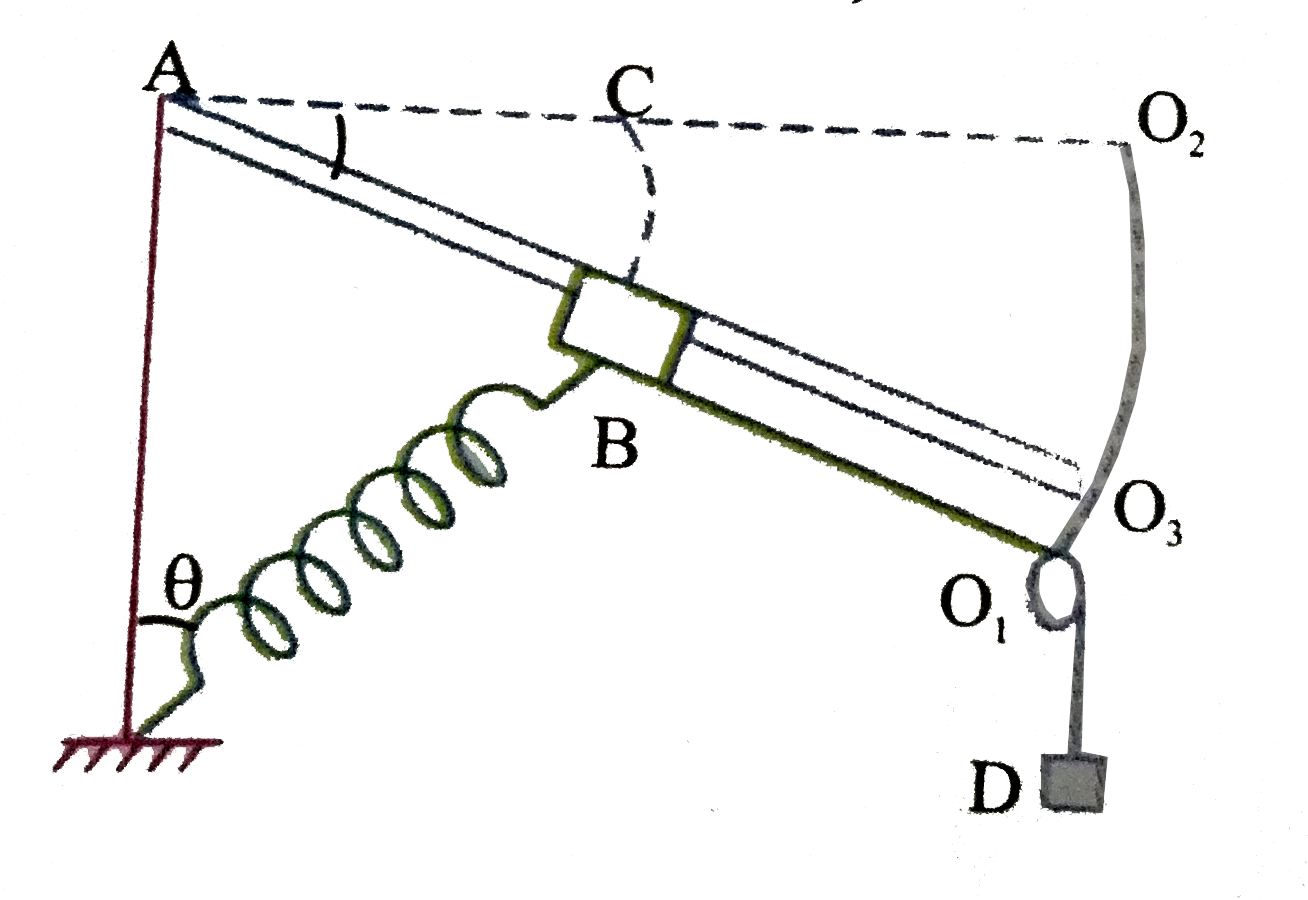 .A⎡⎢ ⎢ ⎢⎣10mgL−KL2(2−√3)28m⎤⎥ ⎥ ⎥⎦12B⎡⎢ ⎢⎣2mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12C⎡⎢ ⎢⎣5mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12D⎡⎢ ⎢⎣6mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12
.A⎡⎢ ⎢ ⎢⎣10mgL−KL2(2−√3)28m⎤⎥ ⎥ ⎥⎦12B⎡⎢ ⎢⎣2mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12C⎡⎢ ⎢⎣5mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12D⎡⎢ ⎢⎣6mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12A sphere is placed on two similar cubes as shown. All surfaces are smooth. When velocity of sphere is 10ms−1 vertical down then find magnitude of velocity of the block B with respect to block C.
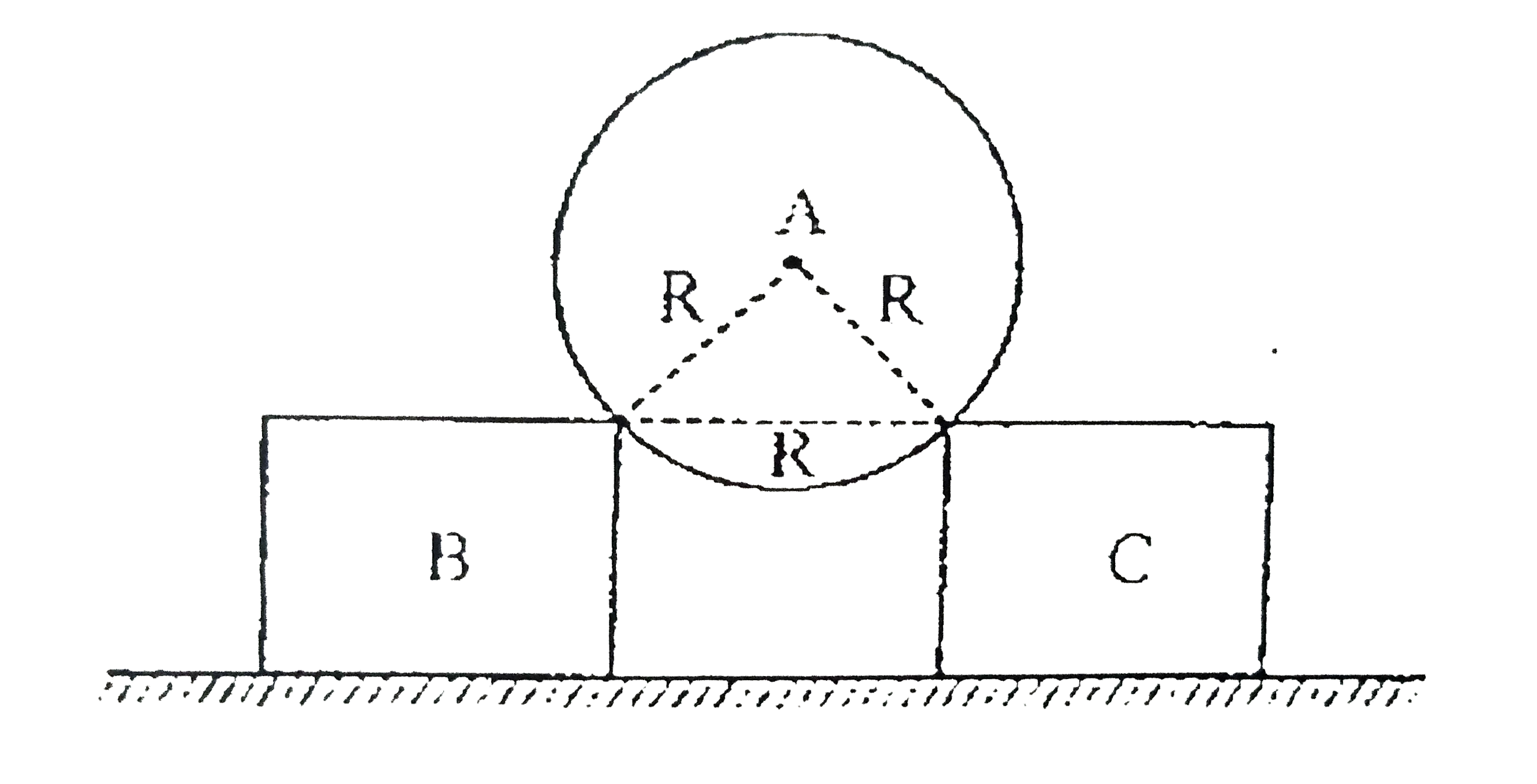 A10√3ms−1B20√3ms−1C30√3ms−1D40√3ms−1
A10√3ms−1B20√3ms−1C30√3ms−1D40√3ms−1
Two blocks A and B of mass m and 2m respectively are moving towards a massive (mass>>2m) cliff with velocities 2v and v respectively. The cliff moves with a velocity v. If the coefficient of restitution of collision at the surface of the cliff is e=1/2, find the:

a. velocity of the block B just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness k which is fitted with the block B.
View SolutionFind out the velocity of block B in a pulley block system as shown in figure.
View SolutionSystem is shown in fig. and wedge is moving toward left with speed 2ms−1. Find the velocity of the block B.

View SolutionThe velocity of A at an instant is 4m/s rightwards. Then the velocity of block B is
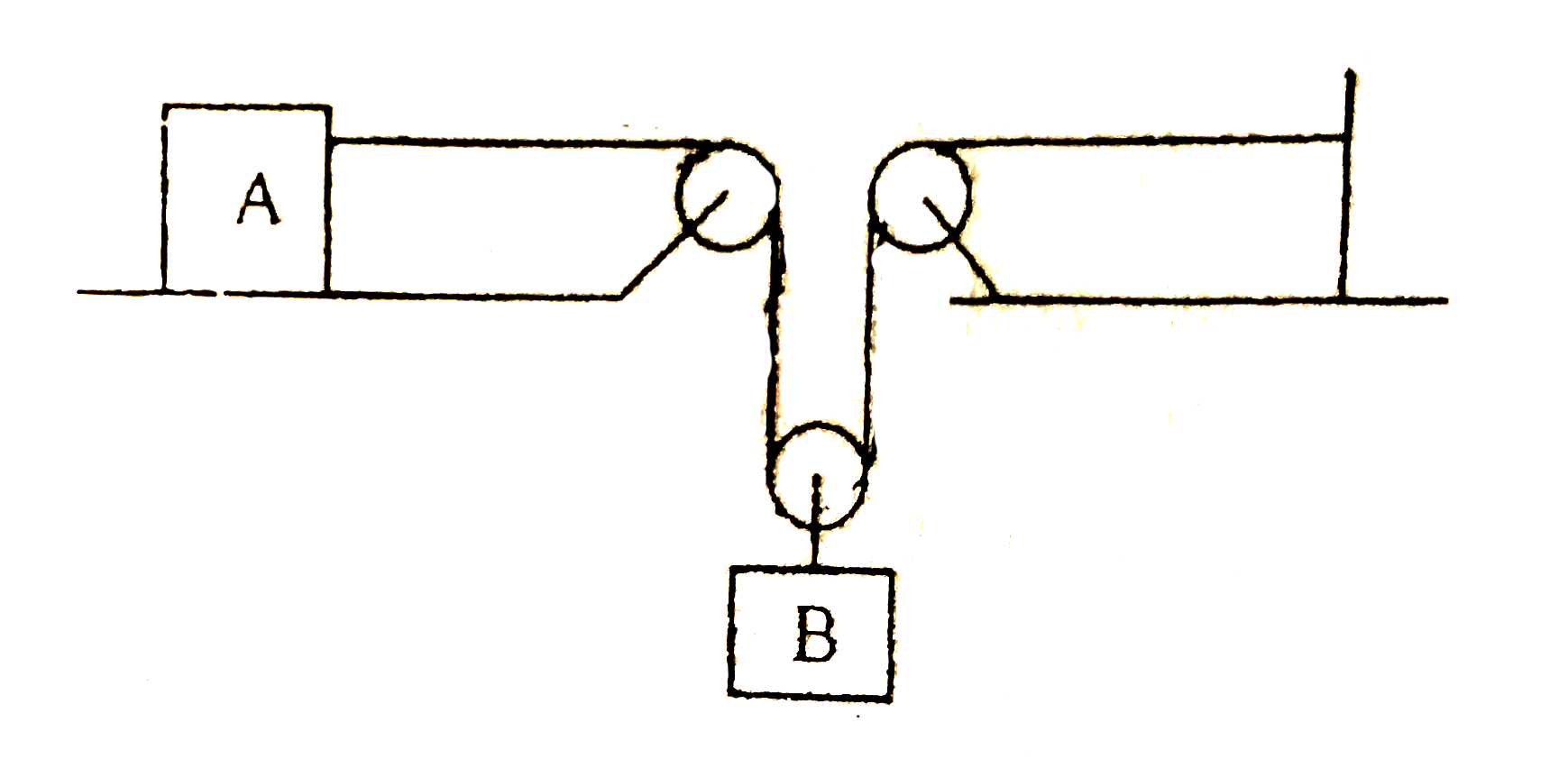
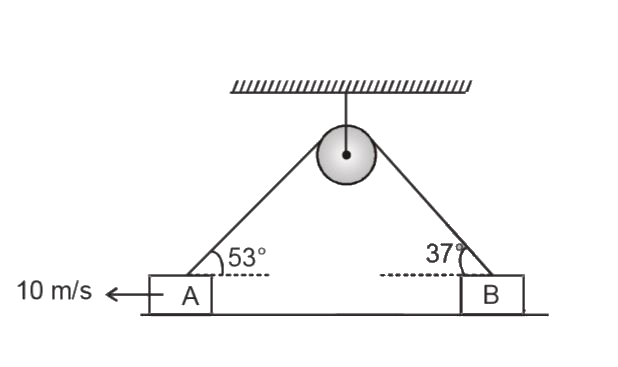
View SolutionIn the arrangement shown, velocity of block A is 10 m/s at a moment. Then the velocity of block B at this instant is :
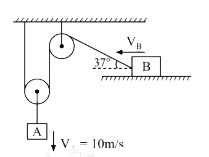
View Solution
