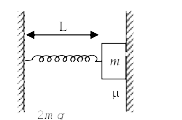
A block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
2mgμ(l−L)
mgμ(l−L)
mg2μ(l−L)
2mgμl
The correct Answer is:B
N=k(l−L)⇒Fmax=μk(l−L)
For equilibrium : mg≤fmax⇒mg≤μk(l−L) ⇒k≥mgμ(l−L)
Similar Questions
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)g - Question 2 - Select One
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4 - Question 3 - Select One
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
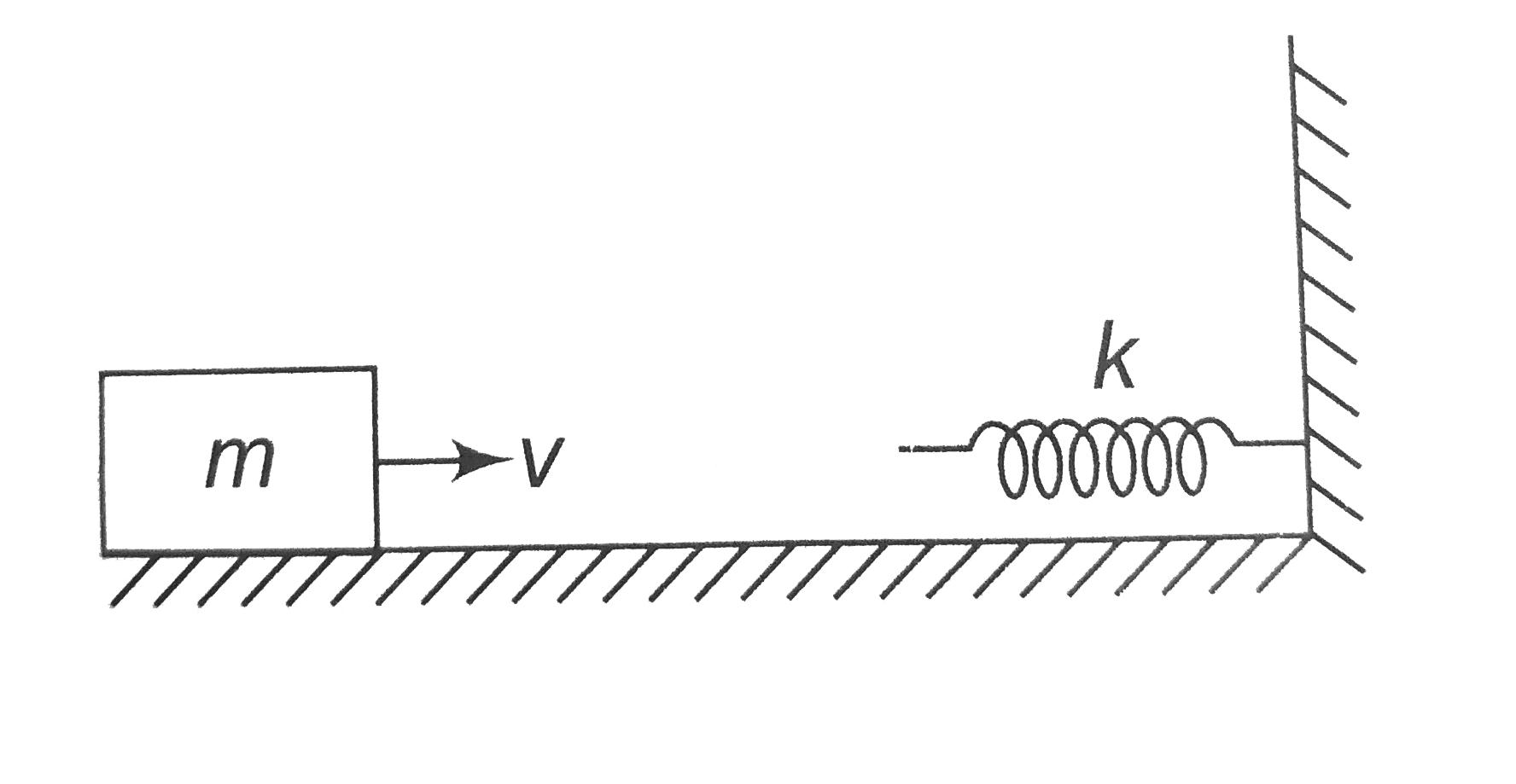 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?
View SolutionIn the equilibrium conditions shown in the figure all the springs have unstretched length l
 View Solution
View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is
 View Solution
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
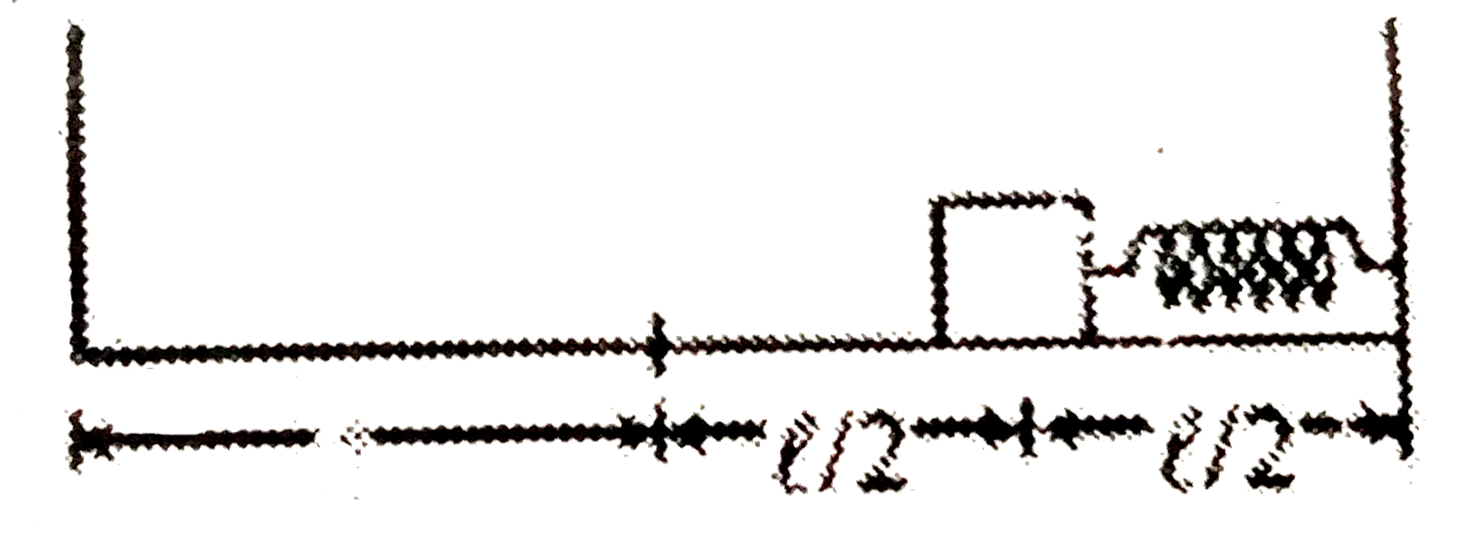 View Solution
View Solution

