Two particles of masses m1 and m2 , m1>m2 move in circular paths under the action of their gravitational attraction. While doing so, their separation remains constant and equals ‘r’. Radius of circular path of m2 is:
r2
m1m2r
m2m1+m2r
m1m1+m2r
The correct Answer is:D
To find the radius of the circular path of mass m2 in a two-particle system where both masses m1 and m2 are in circular motion under their mutual gravitational attraction, we can follow these steps:
1. Understanding the System:
We have two masses, m1 and m2, with m1>m2. They are separated by a distance r and are in circular motion due to their gravitational attraction.
2. Identifying Forces:
The gravitational force between the two masses provides the necessary centripetal force for their circular motion. The gravitational force F can be expressed as:
F=Gm1m2r2
where G is the gravitational constant.
3. Center of Mass:
The center of mass (CM) of the system can be calculated using the formula:
rCM=m1r1+m2r2m1+m2
where r1 is the distance from m1 to the CM, and r2 is the distance from m2 to the CM.
4. Setting up the Distances:
Since the total distance between the two masses is r, we have:
r1+r2=r
5. Relating Distances to Masses:
The distances r1 and r2 can be expressed in terms of the masses:
r1=m2m1r2
Substituting this into the equation for total distance gives:
m2m1r2+r2=r
Factoring out r2:
r2(m2m1+1)=r
6. Solving for r2:
Rearranging the equation to solve for r2:
r2=rm2m1+1=rm2+m1m1=m1rm1+m2
7. Conclusion:
The radius of the circular path of mass m2 is:
r2=m1rm1+m2
Final Answer:
The radius of the circular path of mass m2 is m1rm1+m2.
We have two masses, m1 and m2, with m1>m2. They are separated by a distance r and are in circular motion due to their gravitational attraction.
The gravitational force between the two masses provides the necessary centripetal force for their circular motion. The gravitational force F can be expressed as:
F=Gm1m2r2
where G is the gravitational constant.
The center of mass (CM) of the system can be calculated using the formula:
rCM=m1r1+m2r2m1+m2
where r1 is the distance from m1 to the CM, and r2 is the distance from m2 to the CM.
Since the total distance between the two masses is r, we have:
r1+r2=r
The distances r1 and r2 can be expressed in terms of the masses:
r1=m2m1r2
Substituting this into the equation for total distance gives:
m2m1r2+r2=r
Factoring out r2:
r2(m2m1+1)=r
Rearranging the equation to solve for r2:
r2=rm2m1+1=rm2+m1m1=m1rm1+m2
The radius of the circular path of mass m2 is:
r2=m1rm1+m2
The radius of the circular path of mass m2 is m1rm1+m2.
Similar Questions
_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR - Question 2 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2) - Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2R
For particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
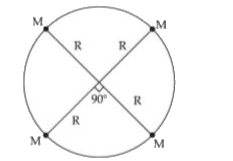 View Solution
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionTwo particles of equal mass m go around a circle of radius R under action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is
View Solution

