The mass density of a spherical body is given by $ρ (r) = \frac{k}{r}$ for $r \leq R$ and $ρ (r) = 0$ for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :

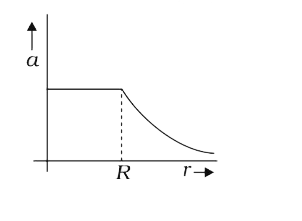
ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem, we need to analyze the mass density of the spherical body and how it affects the acceleration of a test particle at different distances from the center of the sphere.
1. Understanding the Mass Density:
The mass density is given by:
$ρ (r) = \frac{k}{r} for r \leq R$
$ρ (r) = 0 for r > R$
This indicates that the mass density decreases as we move away from the center of the sphere until we reach the radius $R$ .
2. Finding the Mass Inside Radius $r$ :
To find the total mass $M$ within a radius $r$ (where $r \leq R$ ), we need to integrate the density over the volume:
$M = \int_{0}^{r} ρ (r) d V$
The volume element in spherical coordinates is $d V = 4 π r^{2} d r$ . Thus,
$M = \int_{0}^{r} \frac{k}{r} \cdot 4 π r^{2} d r = 4 π k \int_{0}^{r} r d r$
Evaluating the integral:
$M = 4 π k {(\frac{r^{2}}{2})}_{0}^{r} = 2 π k r^{2}$
3. Calculating the Gravitational Field (Acceleration):
The gravitational field $g$ (which is equal to the acceleration $a$ of the test particle) at distance $r$ is given by:
$g = \frac{G M}{r^{2}}$
Substituting $M$ :
$g = \frac{G (2 π k r^{2})}{r^{2}} = 2 π G k$
Thus, for $r \leq R$ , the acceleration $a$ is constant:
$a = 2 π G k$
4. Finding the Mass Outside Radius $R$ :
For $r > R$ , the total mass $M_{1}$ of the sphere can be found by integrating from $0$ to $R$ :
$M_{1} = \int_{0}^{R} \frac{k}{r} \cdot 4 π r^{2} d r = 2 π k R^{2}$
5. Calculating the Gravitational Field for $r > R$ :
The gravitational field for $r > R$ is:
$g = \frac{G M_{1}}{r^{2}} = \frac{G (2 π k R^{2})}{r^{2}}$
Thus, for $r > R$ :
$a = \frac{2 π G k R^{2}}{r^{2}}$
This shows that the acceleration decreases with the square of the distance $r$ .
6. Graphing the Acceleration:
- For $r < R$ , the acceleration $a$ is constant.
- For $r > R$ , the acceleration $a$ decreases as $\frac{1}{r^{2}}$ .
Conclusion:
The correct qualitative graph of acceleration $a$ as a function of distance $r$ will show a constant value for $r < R$ and a decreasing curve for $r > R$ .

Updated on:7/8/2024

Class 12 PHYSICS GRAVITATION

Knowledge Check

Question 1 - Select One
Let there be a spherical symmetric charge density varying as $p (r) = p_{0} \frac{r}{R}$ upto r = R and $ρ (r) = 0$ for $r > R$ , where r is the distance from the origin. The electric field at on a distance $r (r < R)$ from the origin is given by -
A $\frac{ρ_{0} r^{2}}{4 ε_{0} R}$
B $\frac{ρ_{0} r}{4 ε_{0} R}$
C $\frac{ρ_{0} r^{4}}{ε_{0} R}$
D $\frac{ρ_{0} r^{2}}{ε_{0} R}$
Question 2 - Select One
A spherically symmetric gravitational system of particles has a mass density $ρ = {\begin{matrix} ρ_{0} & f or & r & < & R 0 & f or & r & > & R \end{matrix}$ where $ρ_{0}$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce $r (0 < r < O O)$ form the centre of the system is represented by
A
B
C
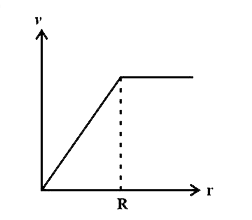D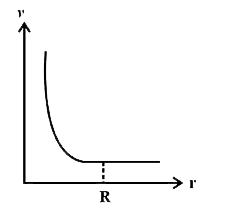
Question 3 - Select One or More
The potential energy function of a particle is given by $U (r) = \frac{A}{2 r^{2}} - \frac{B}{3 r}$ , where $A$ and $B$ are constant and $r$ is the radial distance from the centre of the force. Choose the correct option (s)
AThe equilibrium distance will be $r_{0} = \frac{2 A}{B}$
BThe equilibrium distance will be $r_{0} = \frac{3 A}{B}$
CIf the total energy of the particle is $\frac{B^{2}}{6 A}$ , then its radial velocity will vaishh ate $\frac{r_{0}}{3}$ , where $r_{0}$ is the equilibrium distance
DIf the total energy of the particle is $\frac{B^{2}}{6 A}$ , then its radial velocity will vanish at $\frac{r_{0}}{2}$ ,where $r_{0}$ is the equilibrium distance.

The mass density of a spherical body is given by $ρ (r) = \frac{k}{r}$ for $r \leq R$ and $ρ (r) = 0$ for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :

The correct Answer is:B

Similar Questions

Knowledge Check

Let there be a spherical symmetric charge density varying as $p (r) = p_{0} \frac{r}{R}$ upto r = R and $ρ (r) = 0$ for $r > R$ , where r is the distance from the origin. The electric field at on a distance $r (r < R)$ from the origin is given by -

The potential energy function of a particle is given by $U (r) = \frac{A}{2 r^{2}} - \frac{B}{3 r}$ , where $A$ and $B$ are constant and $r$ is the radial distance from the centre of the force. Choose the correct option (s)

Recommended Questions

The mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :

The correct Answer is:B

Similar Questions

Knowledge Check

Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -

The potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)

Recommended Questions

The mass density of a spherical body is given by $ρ (r) = \frac{k}{r}$ for $r \leq R$ and $ρ (r) = 0$ for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :

Let there be a spherical symmetric charge density varying as $p (r) = p_{0} \frac{r}{R}$ upto r = R and $ρ (r) = 0$ for $r > R$ , where r is the distance from the origin. The electric field at on a distance $r (r < R)$ from the origin is given by -

The potential energy function of a particle is given by $U (r) = \frac{A}{2 r^{2}} - \frac{B}{3 r}$ , where $A$ and $B$ are constant and $r$ is the radial distance from the centre of the force. Choose the correct option (s)