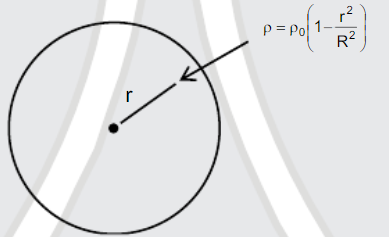
Consider a solid sphere oFIGURE radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oFIGURE a liquid in which it will FIGUREloat is:
ρ03
2ρ05
2ρ03
ρ05
The correct Answer is:2
Step by step video & image solution for Consider a solid sphere oFIGURE radius R and mass density rho(r)=rho_(0)(1-(r^(2))/(R^(2))) 0 lt r le R. The minimum density oFIGURE a liquid in which it will FIGUREloat is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
View Solution
Knowledge Check
A Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
A25ρ0B52ρ0C35ρ0Dρ0sMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
 A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A solid hemisphere of radius R is made to just sink in a liquid of density ρ find theAπR3ρg3BπR3ρg2C0DπR3ρg
The density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
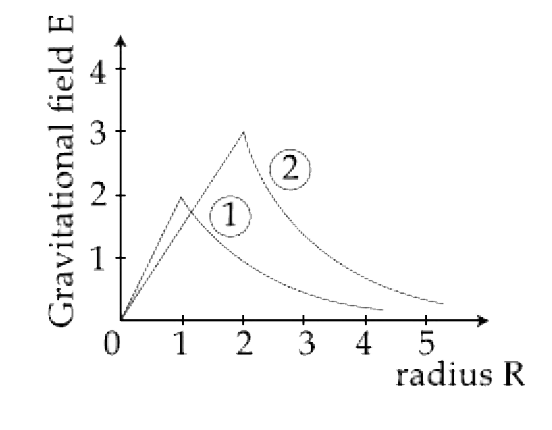
View SolutionConsider two solid sphere oFIGURE radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitional FIGUREield due to sphere 1 and 2 are shown. The value oFIGURE M1M2) is:
View SolutionConsider a spherical symmetric charge distribution with charge density varying as ρ={[ρ0(1−rR),r≤R][0,,r>R]}The electric field at r ,r≤R will be
View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The value of A in terms of Q and R is
View SolutionA solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
View Solution
