A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
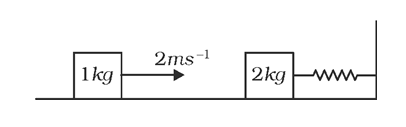
The correct Answer is:2.09
(Momentum conservaation)
Also (Cofficient of restitution)
implies
As 2kg is attached to a spring,
Time taken by 2 kg too return to its initial position is .
Distance move by 1 kg in this time
Similar Questions
A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View Solutionस्प्रिंग स्थिरांक 5X103 N/m का एक स्प्रिंग प्रारंभ में बिना खिंचाव वाली स्थिति से 10 सेमी तक खींचा जाता है। फिर, इसे और 10 सेमी और बढ़ाने के लिए आवश्यक कार्य है
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View Solution
