A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
The correct Answer is:A
hAB=r−rcos(90∘−θ)=r−rsinθ
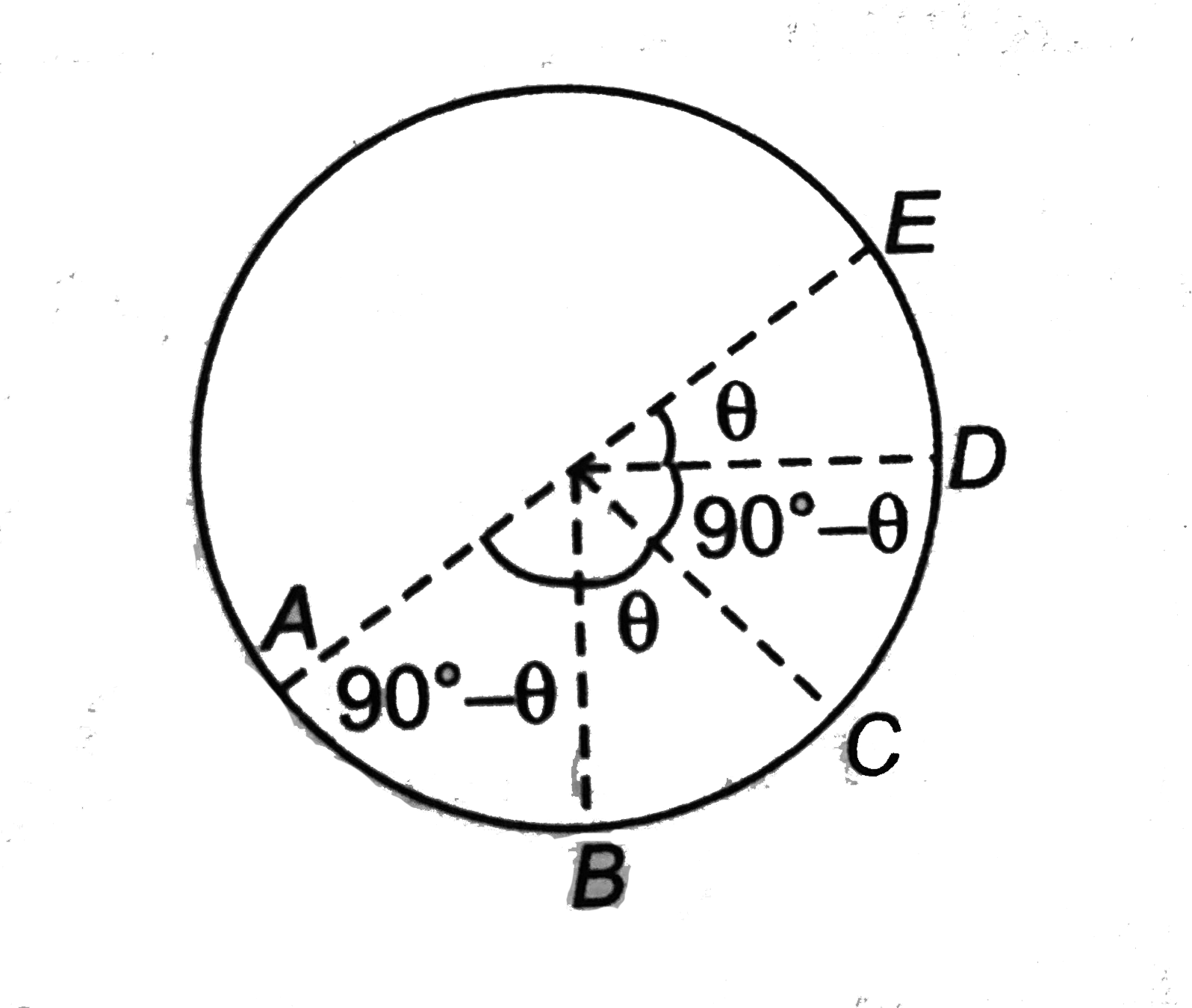
hBC=r−rcosθ
hCD=rsin(90∘−θ)=rcosθ
hDE=rsinθ
Writing pressure equation between points Aand E we have
pA+(r−rsinθ)ρg−(r−rcosθ)−ρg−(rcosθ)(σ)g−(rsinθ)σg=pE
But pA=pE=pgas
Solving this equation, we get
tanθ=(ρ−σρ−σ)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.1
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

View SolutionA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is

View SolutionTwo non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
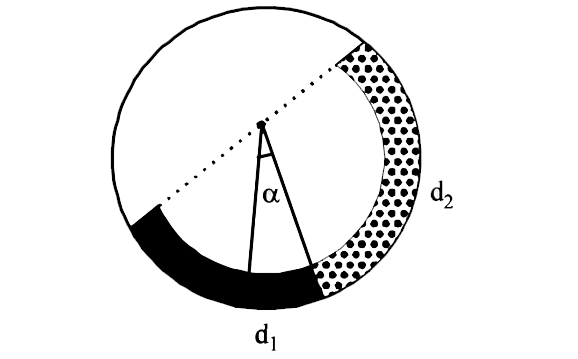
View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
View SolutionFind the equation to the circle which passes through the points (1,2)(2,2) and whose radius is 1.
View SolutionFind the equation of a circle of radius 5 whose centre lies on x-axis and passes through the point (2,3).
View SolutionFind the equation of the circle with radius 5 whose center lies on the x-axis and passes through the point (2, 3).
View SolutionFind the equation of a circle of radius 5 units whose centre lies on x-axis and passes through the point (2, 3).
View SolutionA hemispherical bowl of radius R si set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
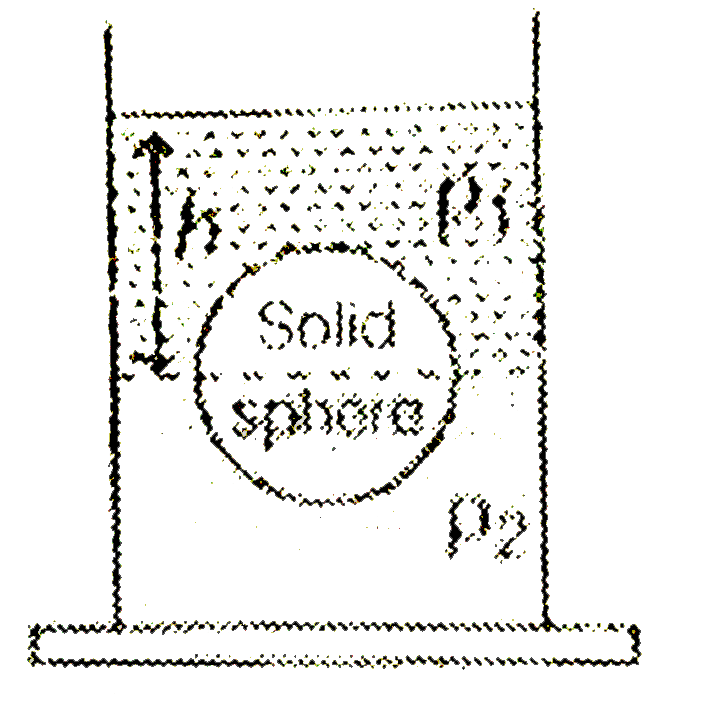
View Solution