Time interval for which the detector remains idle in each cycle of intensity
13sec
23sec
12sec
14sec
The correct Answer is:A, C, D
To solve the problem of determining the time interval for which the detector remains idle in each cycle of intensity, we can follow these steps:
Step 1: Understand the Problem
We have two sound sources with frequencies f1=400Hz and f2=401Hz. The detector can only detect sound when the amplitude of the resultant wave is greater than A.
Step 2: Write the Equations for the Waves
The equations for the waves emitted by the two sources can be written as:
- For source 1: y1=Asin(2πf1t)
- For source 2: y2=Asin(2πf2t)
Step 3: Find the Resultant Amplitude
The resultant amplitude when both waves interfere can be expressed as:
Aresultant=2Acos(π(f1−f2)t)
Given f1−f2=−1Hz, we can simplify this to:
Aresultant=2Acos(πt)
Step 4: Set the Condition for Detection
The detector will only detect the sound when the amplitude is greater than A. Thus, we set up the inequality:
2Acos(πt)>A
Dividing both sides by A (assuming A>0):
2cos(πt)>1
This simplifies to:
cos(πt)>12
Step 5: Solve for t
The condition cos(πt)>12 corresponds to the angles where the cosine function is greater than 12. The angles satisfying this condition are:
−π3<πt<π3and5π3<πt<7π3
Dividing through by π:
−13<t<13and53<t<73
Step 6: Determine the Idle Time
The detector is idle when cos(πt)≤12:
1. From t=13 to t=53, the detector is idle.
2. The time interval for which the detector is idle is:
Δt=53−13=43seconds
Final Result
The time interval for which the detector remains idle in each cycle of intensity is 43seconds.
---
We have two sound sources with frequencies f1=400Hz and f2=401Hz. The detector can only detect sound when the amplitude of the resultant wave is greater than A.
The equations for the waves emitted by the two sources can be written as:
- For source 1: y1=Asin(2πf1t)
- For source 2: y2=Asin(2πf2t)
The resultant amplitude when both waves interfere can be expressed as:
Aresultant=2Acos(π(f1−f2)t)
Given f1−f2=−1Hz, we can simplify this to:
Aresultant=2Acos(πt)
The detector will only detect the sound when the amplitude is greater than A. Thus, we set up the inequality:
2Acos(πt)>A
Dividing both sides by A (assuming A>0):
2cos(πt)>1
This simplifies to:
cos(πt)>12
The condition cos(πt)>12 corresponds to the angles where the cosine function is greater than 12. The angles satisfying this condition are:
−π3<πt<π3and5π3<πt<7π3
Dividing through by π:
−13<t<13and53<t<73
The detector is idle when cos(πt)≤12:
1. From t=13 to t=53, the detector is idle.
2. The time interval for which the detector is idle is:
Δt=53−13=43seconds
The time interval for which the detector remains idle in each cycle of intensity is 43seconds.
Similar Questions
Two radio stations broadcast their programmes at the same amplitude A and at slightly different frequencies ω1 and ω2 respectively, where ω1−ω2=103HzA detector receives the signals from the two stations simultaneously. it can only detect signals of intensity ≥2A2.
(i) Find the time interval between successive maxima of the intensity of the signal received by the detector.
(ii) Find the time for which the detector remains idle in each cycle of the intensity of the signal.
View SolutionTwo radio stations broadcast their programmes at the same amplitude A, and at slightly different frequencies ω1andω2 respectively , where ω2−ω1=103Hz. A detector receives the signals from the two stations simultaneously . It can emit signals only of intensity ≥2A2.
(i). Find the time intervals between successive maxima of the intensity of the signal received by the detector .
ii. Find the time for which the detector remains idle in each cycle of the intensity of the signal .
View Solution
Knowledge Check
A train normally coveres a certain distance at a speed of 60 km/hr. However, if it were to halt for a fixed time interval in each hour its average speed reduced to 50 km/hr. What is the time interval for which the train halt in each hour ?
A10 minutesB20 minutesC6 minutesD12 minutesA train normally covers a certain distance at a speed of 60 km/hr. However, if it were to halt for a fixed time interval in each hour its average speed reduced to 50km/hr. what is the time interval for which the train halt in each hour?
A10 minutesB20 minutesC6 minutesD12 minutesThe dimensions of time in Electrical intensity is
A−1B−2C−3D3
Three plane sources of sound of frequency n1 = 400 Hz, 401 Hz and n3 = 402 Hz of equal amplitude a each, are sounded together. A detector receives waves from all the three sources simultaneously. It can detect signals of amplitude gt A. Calculate
(a) period ofone complete cycle of intensity received by the detector and
(b) time for which the detector remains idle in each cycle of intensity.
View SolutionAn ideal gas is pumped into a rigid container having diathermic walls so that the tempreture remains constant. In a certain time interval energy of the contains of the container also doubled in the interval?
View SolutionTwo radio signal broadcast their program at the same amplitude A and at slightly different frequency ω1,ω2 respectively given that ω2−ω1=π×102. A detector detects the signal from the two stations simultaneously. It can only detect signal of in intensiy ≥3A2. Detector remains idle for time t0=αβ×10−2 sec in each cycle of the intensity of the signal. Here α and β are integers. Find minimum value of α+β.
View Solution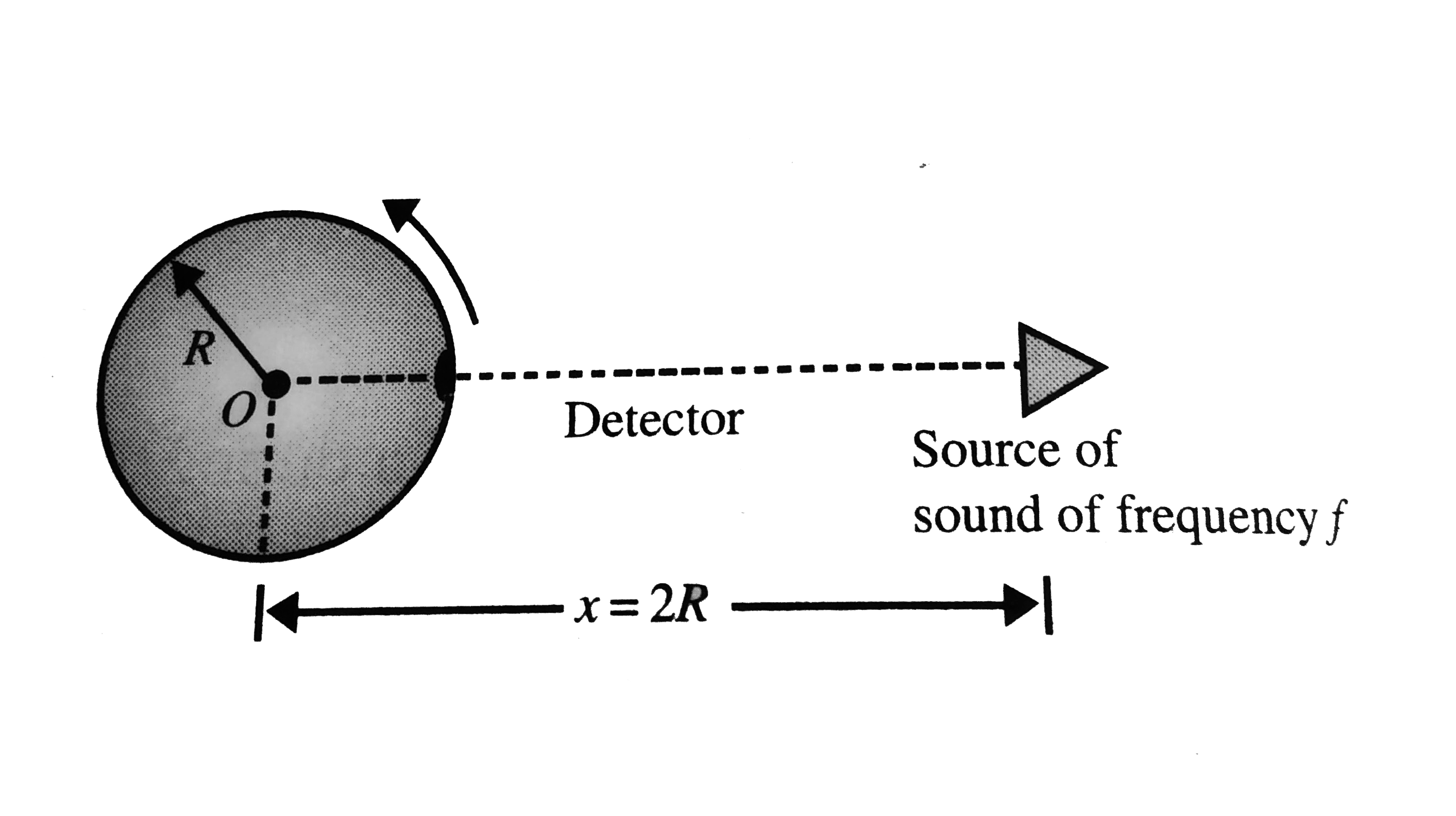
A source of sound and detector are arranged as shown in Fig. The detector is moving along a circle with constant angular speed ω. It start from the shown location in anticlockwise direction at t=0
(Take velocity of sound in air as v)
Q. Find the time at which the detector will hear the maximum frequency for the first time.
View SolutionTwo coherent sound sources A and B produce a sound of wavelength λ. If at t=0 a detector starts moving with constant velocity v0 from point O along y - direction, then the minimum time, after which it detects the sound of maximum intensity, is (D>>λ)
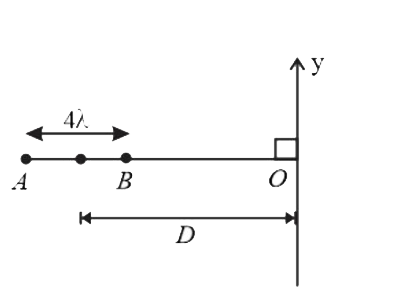
View Solution
