Acceleration of a particle has a value 'a' for a time t. It is followed immediately by a retardation of magnitude 'a' for time t/2. Consider this as one cycle. Initial velocity of particle was zero. The displacement of the particle after n such cycles in succession is:
n(3n+4)8at2
n(n+1)2at2
(n2+n+1)4at2
nat2
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the particle during the cycles of acceleration and retardation.
Step 1: Understanding the Motion
The particle undergoes two phases in each cycle:
1. Acceleration phase: The particle accelerates with an acceleration a for a time t.
2. Retardation phase: The particle then decelerates (retardation) with a magnitude of a for a time t2.
Step 2: Finding the Velocity at the End of One Cycle
- Initial velocity u=0.
- After the acceleration phase for time t:
v1=u+at=0+at=at
- During the retardation phase for time t2:
v2=v1−a(t2)=at−a(t2)=at−at2=at2
Thus, the velocity at the end of one complete cycle is v=at2.
Step 3: Displacement During One Cycle
- Displacement during the acceleration phase:
s1=ut+12at2=0+12at2=12at2
- Displacement during the retardation phase:
s2=v1(t2)−12a(t2)2=at(t2)−12a(t2)2
s2=at22−12a(t24)=at22−at28=4at28−at28=3at28
- Total displacement in one cycle:
scycle=s1+s2=12at2+38at2=48at2+38at2=78at2
Step 4: Total Displacement After n Cycles
Since the displacement in each cycle is the same, the total displacement after n cycles is:
stotal=n⋅scycle=n⋅78at2=7n8at2
Final Answer
The displacement of the particle after n cycles is:
7n8at2
The particle undergoes two phases in each cycle:
1. Acceleration phase: The particle accelerates with an acceleration a for a time t.
2. Retardation phase: The particle then decelerates (retardation) with a magnitude of a for a time t2.
- Initial velocity u=0.
- After the acceleration phase for time t:
v1=u+at=0+at=at
- During the retardation phase for time t2:
v2=v1−a(t2)=at−a(t2)=at−at2=at2
Thus, the velocity at the end of one complete cycle is v=at2.
- Displacement during the acceleration phase:
s1=ut+12at2=0+12at2=12at2
- Displacement during the retardation phase:
s2=v1(t2)−12a(t2)2=at(t2)−12a(t2)2
s2=at22−12a(t24)=at22−at28=4at28−at28=3at28
- Total displacement in one cycle:
scycle=s1+s2=12at2+38at2=48at2+38at2=78at2
Since the displacement in each cycle is the same, the total displacement after n cycles is:
stotal=n⋅scycle=n⋅78at2=7n8at2
The displacement of the particle after n cycles is:
7n8at2
Similar Questions
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe displacement x of a particle varies as
√x=t−2
(i) What is the velocity and acceleration of the particle at t=0?
(ii) When will the velocity of the particle become zero?
(iii) What is the displacement of the particle when its velocity is zero?
(iv) Is the motion of the particle uniformly accelerated or not?
View Solution
Knowledge Check
The velocity of a particle is zero at time t = 2s, then
Adisplacement must be zero in the interval t = 0 to t = 2 s.Bacceleration may be zero at t = 2 s.Cvelocity must be zero for t>2s .Dacceleration must be zero at t = 2 s.A particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
AAB4AC8ADzeroThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.A41m/sB4m/sC39m/sD27m/s
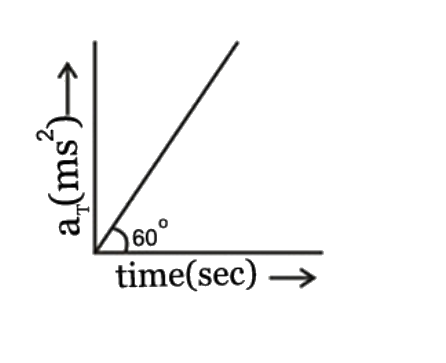
Tangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
View SolutionThe displacement of a particle in time t is given by s=2t2−3t+1. The acceleration is
View SolutionPower supplied to a particle of mass 2 kg varies with time as P=3t22W, where t is in seconds. If velocity of particle at t=0 is zero, then the velocity of particle at t=2 s will be
View SolutionA particle moves according to the law x=t3−6t2+9t+5. The displacement of the particle at the time when its acceleration is zero, is
View SolutionA particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
View Solution
