The relation between time and distance is is : a=(4−2x) .Select the correct alternative (s) .
Particle further comes to rest at x = 4
Particle oscillates about x = 2
Maximum speed of particle is 4 units
All of the above
The correct Answer is:A, B
To solve the problem, we start with the given relation between time and distance, which is a=4−2x. This equation describes the acceleration a of a particle as a function of its position x.
1. Understanding the Relation:
The equation a=4−2x indicates that the acceleration of the particle depends on its position x.
2. Finding Velocity:
We know that acceleration a can be expressed as the derivative of velocity v with respect to position x:
a=dvdt=dvdx⋅dxdt=vdvdx
Therefore, we can rewrite the equation as:
vdvdx=4−2x
3. Integrating to Find Velocity:
We can separate variables and integrate:
vdv=(4−2x)dx
Integrating both sides:
∫vdv=∫(4−2x)dx
This gives us:
v22=4x−x2+C
where C is the constant of integration.
4. Finding the Maximum Speed:
To find the maximum speed, we need to find the critical points of v. We can do this by differentiating v2 with respect to x and setting it to zero:
ddx(4x−x2)=4−2x=0
Solving for x:
2x=4⟹x=2
5. Calculating Maximum Speed:
Substitute x=2 back into the equation for v2:
v2=2(4⋅2−22)=2(8−4)=2⋅4=8
Thus, the maximum speed v is:
v=√8=2√2
6. Determining Oscillation:
The particle oscillates about x=2 because the acceleration changes sign at this point, indicating that it is a point of equilibrium. The particle will oscillate between x=0 and x=4.
Conclusion:
The correct statements are:
1. The maximum speed of the particle is 2√2 at x=2.
2. The particle oscillates about x=2.
The equation a=4−2x indicates that the acceleration of the particle depends on its position x.
We know that acceleration a can be expressed as the derivative of velocity v with respect to position x:
a=dvdt=dvdx⋅dxdt=vdvdx
Therefore, we can rewrite the equation as:
vdvdx=4−2x
We can separate variables and integrate:
vdv=(4−2x)dx
Integrating both sides:
∫vdv=∫(4−2x)dx
This gives us:
v22=4x−x2+C
where C is the constant of integration.
To find the maximum speed, we need to find the critical points of v. We can do this by differentiating v2 with respect to x and setting it to zero:
ddx(4x−x2)=4−2x=0
Solving for x:
2x=4⟹x=2
Substitute x=2 back into the equation for v2:
v2=2(4⋅2−22)=2(8−4)=2⋅4=8
Thus, the maximum speed v is:
v=√8=2√2
The particle oscillates about x=2 because the acceleration changes sign at this point, indicating that it is a point of equilibrium. The particle will oscillate between x=0 and x=4.
The correct statements are:
1. The maximum speed of the particle is 2√2 at x=2.
2. The particle oscillates about x=2.
Similar Questions
Knowledge Check
Select the correct alternatives :
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.Acceleration of a particle which is at rest at x=0 is →a=(4−2x)ˆi. Select the correct alternative (s).
AMaximum speed of the particle is 4 unitsBParticle further comes to rest at x=4CParticle oscillates about x=2DParticle will continuously acceleration along the x-axis.For the given circuit, select the correct alternative(s)
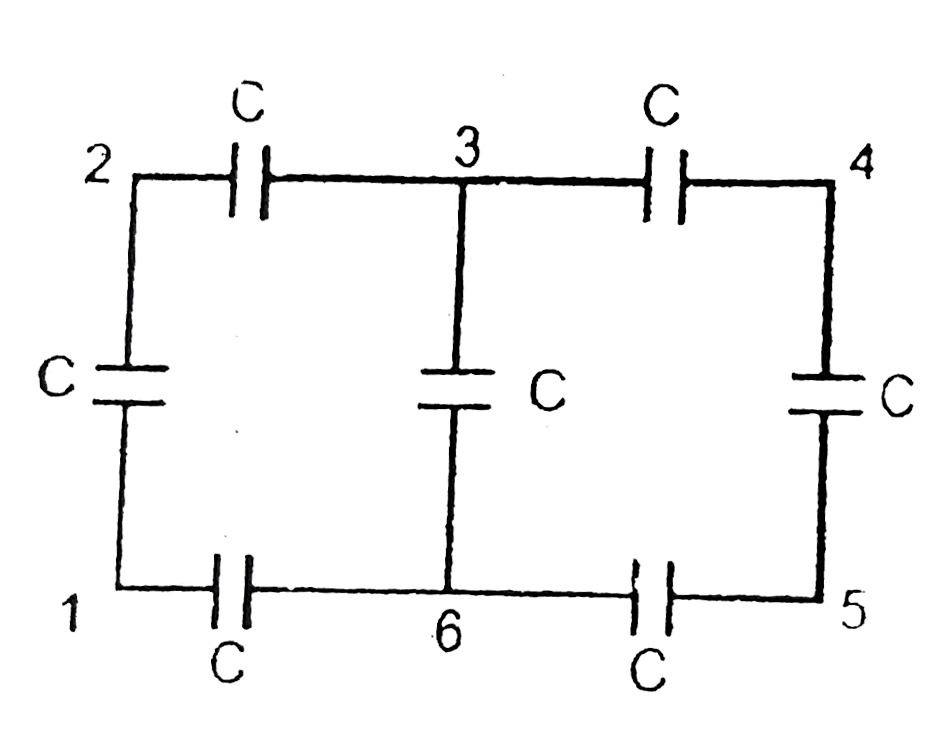 AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
The equational of a stationary wave in a string is y=(4mm)sin[(314m−1x]cosωt. Select the correct alternative (s).
View SolutionIn the arrangement shown in figure all surface are amoth .Select the correct alternative(s).

View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
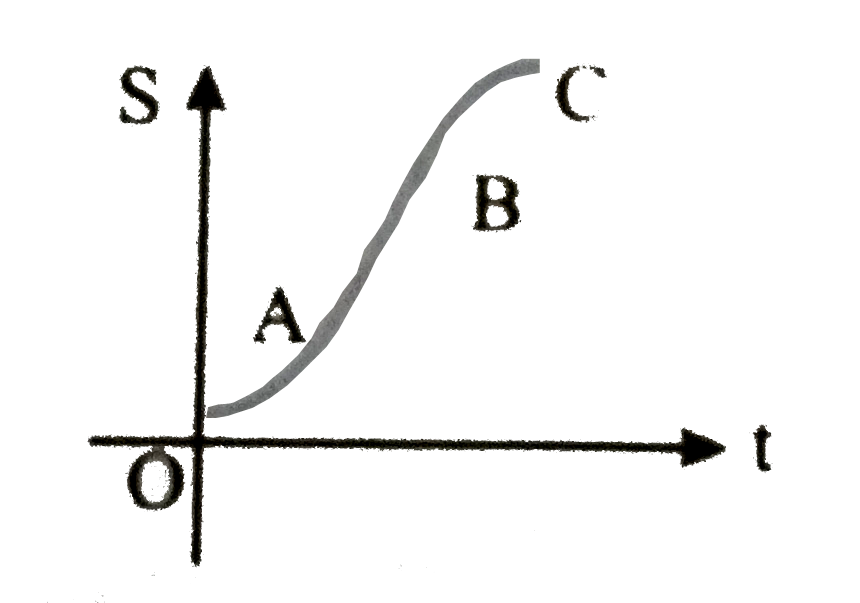 .
.
View SolutionAcceleration time graph of a particle executing SHM is as shown in the figure. Select the correct alternative (s)
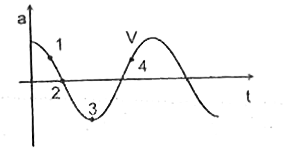
View Solution
