An electric dipole is placed at the centre of a sphere. Select the correct alternative(s).
The flux of electric field through the sphere is zero
The electric field is zero at every point of the sphere
The electric field is not zero anywhere on the sphere
The electric field is zero on a circle on the sphere
The correct Answer is:A, C
To solve the problem regarding the electric dipole placed at the center of a sphere, we will analyze the statements provided and determine which ones are correct based on the principles of electrostatics.
1. Understanding the Setup:
- We have an electric dipole consisting of two charges: a positive charge (+q) and a negative charge (-q) separated by a distance 'd'. This dipole is placed at the center of a sphere.
2. Electric Flux through the Sphere:
- The electric flux (Φ) through a closed surface is given by Gauss's law, which states that Φ = Q_enc/ε₀, where Q_enc is the total charge enclosed by the surface and ε₀ is the permittivity of free space.
- In this case, the dipole does not enclose any net charge because the positive and negative charges cancel each other out (Q_enc = +q - q = 0).
- Therefore, the electric flux through the sphere is zero (Φ = 0).
3. Electric Field Inside the Sphere:
- While the electric flux through the sphere is zero, it does not imply that the electric field (E) is zero at every point inside the sphere. The electric field due to a dipole exists at various points in space, including inside the sphere.
- The electric field is not uniform and varies with position, but it is not zero anywhere inside the sphere.
4. Analyzing the Statements:
- Statement 1: The flux of electric field through the sphere is zero. (Correct)
- Statement 2: Electric field is zero at every point of the sphere. (Incorrect)
- Statement 3: Electric field is not zero at every point of the sphere. (Correct)
- Statement 4: Electric field is zero on a circle. (Incorrect)
5. Conclusion:
- The correct alternatives are Statement 1 and Statement 3.
- We have an electric dipole consisting of two charges: a positive charge (+q) and a negative charge (-q) separated by a distance 'd'. This dipole is placed at the center of a sphere.
- The electric flux (Φ) through a closed surface is given by Gauss's law, which states that Φ = Q_enc/ε₀, where Q_enc is the total charge enclosed by the surface and ε₀ is the permittivity of free space.
- In this case, the dipole does not enclose any net charge because the positive and negative charges cancel each other out (Q_enc = +q - q = 0).
- Therefore, the electric flux through the sphere is zero (Φ = 0).
- While the electric flux through the sphere is zero, it does not imply that the electric field (E) is zero at every point inside the sphere. The electric field due to a dipole exists at various points in space, including inside the sphere.
- The electric field is not uniform and varies with position, but it is not zero anywhere inside the sphere.
- Statement 1: The flux of electric field through the sphere is zero. (Correct)
- Statement 2: Electric field is zero at every point of the sphere. (Incorrect)
- Statement 3: Electric field is not zero at every point of the sphere. (Correct)
- Statement 4: Electric field is zero on a circle. (Incorrect)
- The correct alternatives are Statement 1 and Statement 3.
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - COMPREHENSION BASED (COMPREHENSION - II)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - (PROBLEM SOLUTION) COMPREHENSION - I (COMPREHENSION BASED TYPE)
3 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
24 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
Knowledge Check
Select the correct alternatives :
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.An electric dipole is placed at the centre of a sphere. Mark the correct options:
AThe electric field is zero at every point of the sphere.BThe flux of the electric field through the sphere is non-zero.CThe electric field is zero on a circle on the sphere.DThe electic field is not zero anywhere on the sphere.An electric dipole is placed at the centre of a sphere. Mark the correct options:
Athe electric field is zero at every point of the spereBthe flux of the electric field through to the sphere is zeroCthe electric field is not zero at anywhere on the sphereDboth (2) and (3)
An electric diposle is placed at the cetre of a sphere . Mark the correct answer .
View SolutionAn electric dipole is placed at the centre of a sphere. Find the electric flux passing through the sphere.
View SolutionGiven below are two statements :
Statement I : An electric dipole is placed at the centre of a hollow sphere. The flux of electric field through the sphere is zero but the electric field is not zero anywhere in the sphere.
Statement II : If R is the radius of a solid metallic sphere and Q be the total charge on it. The electric field at any point on the spherical surface of radius r(<R) is zero but the electric flux passing through this closed spherical surface of radius r is not zero.
In the light of the above statements, choose the correct answer from the options given below :
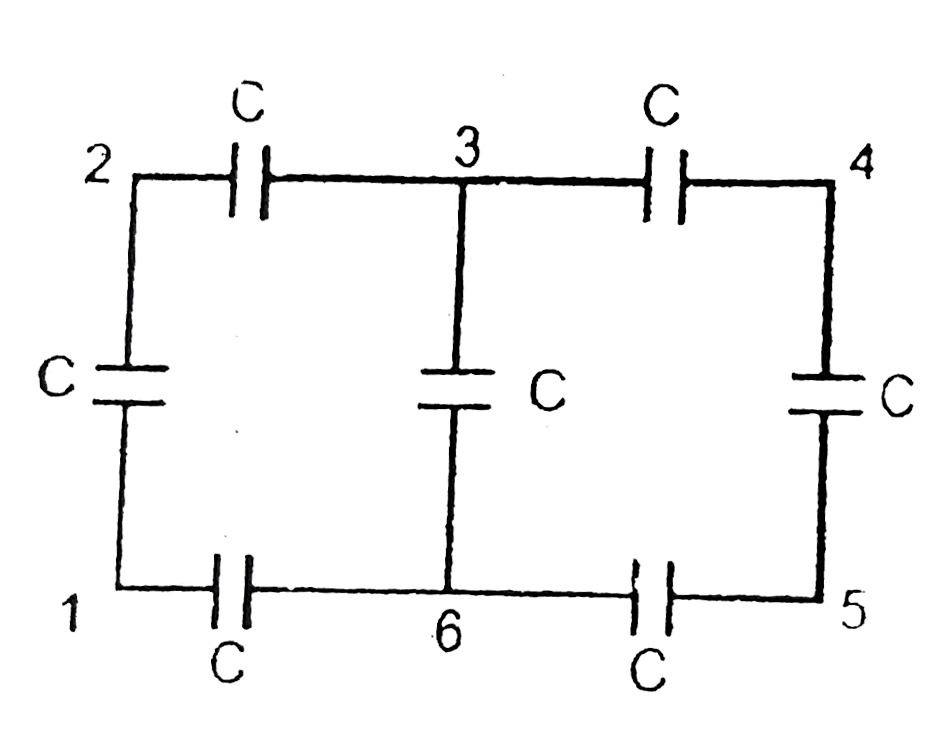
View SolutionFor the given circuit, select the correct alternative(s)
View SolutionA short electric dipole is placed along y-axis at the origin. The electric field vector at a point P on x-axis is →E1. The dipole is rotated by π2 at its position . Now, the electric field vector at point P is →E2. Select the correct alternative(s) :
View Solution
