Consider the curves given by the following quadratic function.
f1(x)=5x2+2x+1,f2(x)=5x2+6x+1
f3(x)=x2−7x+6,f4(x)=64x2+48x+9
If A1,A2,A3andA4 denote the lengths of the intercepts on the X-axis made by the above curve respectively, then which of the following is true?Solution in Telugu
A1>A2>A3>A4>0
A4<A2<A3
A3<A2<A4
A2<A4<A3
The correct Answer is:B
Step by step video, text & image solution for Consider the curves given by the following quadratic function. f_(1)(x)=5x^(2)+2x+1,f_(2)(x)=5x^(2)+6x+1 f_(3)(x)=x^(2)-7x+6,f_(4)(x)=64x^(2)+48x+9 If A_(1),A_(2),A_(3)andA_(4) denote the lengths of the intercepts on the X-axis made by the above curve respectively, then which of the following is true? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the domain of the real function f(x)=1√[x]2−[x]−2.
View SolutionConsider the fucntion ,f_(1)(x)=sqrt(|x|)f_(2)(x)=sqrt(x);f_(3)(x)=x^((1)/(3))f_(4)(x)=(x^(2))^((1)/(3))
View SolutionLet f_(1)(x)={x,x 1 and 0 otherwise f_(2)(x)=f_(1)(-x) for all x abd f_(3)(x)=-f_(2)(x) for all x and f_(4)(x)=-f_(3)(-x) for all x Which of the following is necessarily true?
View SolutionLet f1:R→Randf2:C→C are two functions such that f1(x)=x3andf2=x3.Prove that f1andf2are not same.
View SolutionFor x in R-{0,1}, let f_(1)(x)=(1)/(x),f_(2)(x)=1-x and f_(3)(x)=(1)/(1-x) be three given functions.If a function,J(x) satisfies (f_(2)oJ_(o)f_(1))(x)=f_(3)(x) then J(x) is equal to:
View SolutionA deuteron and an alpha -particle are placed in an electric field.The forces acting on them are F_(1) and F_(2) and their accelerations are a_(1) and a_(2) respectively. (i) F_(1) = F_(2) (ii) F_(1) != F_(2) (iii) a_(1) = a_(2) (iv) a_(1) != a_(2)
View SolutionFor x∈R−{0,1}, let f1(x)=1x,f2(x)=1−xandf3(x)=11−x be three given functions. If a function, J(x) satisfies (f2∘J∘f1)(x)=f3(x), then J(x) is equal to
View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R. then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
View SolutionIf f1(x)=2x+3,f2(x)=3x2+5,f3(x)=x+cosx are defined from R→R, then f1,f2 and f3 are
View SolutionSupposed that f_(1):RtoR,f_(2):[0,oo)toR,f_(3):RtoR And f_(4):rto[0,oo) As follows f_(1)(x)={((|x),यदि,xlt0),(e^(x),यदि,xge0):} f_(2)(x)=x^(2) f_(3)(x)={(sinx, यदि,xlt0),(x, यदि,xge0):} And f_(a)(x)={(f_(2)(f_(1)(x)),यदि,xlt0),(f_(2)(f_(1)(x))-1,यदि ,xge0):}
View Solutionयदि D(x)=f1(x)f2(x)f3(x)a2b2c2a3b3c3 जहाँ f1,f2,f3 अवकलनीय फलन तथा a2,b2,c2,b3,c3 अचर है।
I : D(x)=∫f1(x)dx∫f2(x)dx∫f3(x)dxa2b2c2a3b3c3+c
-II : कुछ फलनों के योग का समाकलन, प्रत्येक फलन के समाकलन के योग के बराबर होता है।
View SolutionFor x∈R,x≠0,x≠1, let f0(x)=11−x and fn+1(x)=f0(fn(x)),n=0,1,2,.... Then the value of f100(3)+f1(23)+f2(32) is equal to
View Solutionफलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
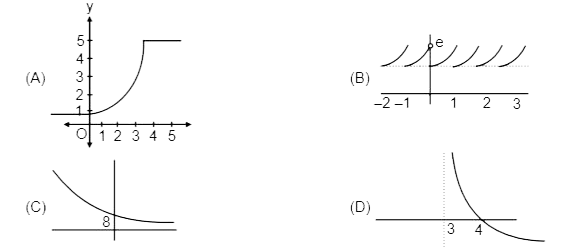
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
View SolutionIf f1(x)=2x+3,f2(x)=3x2+5,f3(x)=x+cosx are defined from R→R, then f1,f2 and f3 are
View Solution
