A deuteron and an α-particle are placed in an electric field.The forces acting on them are F1 and F2 and their accelerations are a1 and a2 respectively.
(i) F1=F2
(ii) F1≠F2
(iii) a1=a2
(iv) a1≠a2
F1=F2
F1>F2
a1=a2
a_(1) cancel(=) a_(2)
The correct Answer is:3
To solve the problem, we need to analyze the forces and accelerations acting on a deuteron and an alpha particle placed in an electric field.
1. Identify the Charges:
- A deuteron consists of one proton and one neutron, giving it a charge of +e (where e is the elementary charge).
- An alpha particle consists of two protons and two neutrons, giving it a charge of +2e.
2. Determine the Forces:
- The force F acting on a charged particle in an electric field E is given by the equation:
F=qE
- For the deuteron:
F1=q1E=eE
- For the alpha particle:
F2=q2E=2eE
3. Compare the Forces:
- Since F1=eE and F2=2eE, we can see that:
F1≠F2
- Therefore, the forces acting on the deuteron and the alpha particle are not equal.
4. Determine the Masses:
- The mass of a deuteron is approximately 2m (where m is the mass of a proton).
- The mass of an alpha particle is approximately 4m.
5. Calculate the Accelerations:
- Using Newton's second law F=ma, we can express the accelerations:
a1=F1m1=eE2m
a2=F2m2=2eE4m=eE2m
- From the above equations, we see that:
a1=a2
- Therefore, the accelerations of the deuteron and the alpha particle are equal.
Conclusion:
- From the analysis, we conclude:
- (ii) F1≠F2 (the forces are not equal)
- (iii) a1=a2 (the accelerations are equal)
Final Answer:
The correct options are (ii) and (iii).
- A deuteron consists of one proton and one neutron, giving it a charge of +e (where e is the elementary charge).
- An alpha particle consists of two protons and two neutrons, giving it a charge of +2e.
- The force F acting on a charged particle in an electric field E is given by the equation:
F=qE
- For the deuteron:
F1=q1E=eE
- For the alpha particle:
F2=q2E=2eE
- Since F1=eE and F2=2eE, we can see that:
F1≠F2
- Therefore, the forces acting on the deuteron and the alpha particle are not equal.
- The mass of a deuteron is approximately 2m (where m is the mass of a proton).
- The mass of an alpha particle is approximately 4m.
- Using Newton's second law F=ma, we can express the accelerations:
a1=F1m1=eE2m
a2=F2m2=2eE4m=eE2m
- From the above equations, we see that:
a1=a2
- Therefore, the accelerations of the deuteron and the alpha particle are equal.
- From the analysis, we conclude:
- (ii) F1≠F2 (the forces are not equal)
- (iii) a1=a2 (the accelerations are equal)
The correct options are (ii) and (iii).
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTION( ONLY ONE ANSWER)
12 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-C ( OBJECECTIVE TYPE QUESTIONS)
2 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
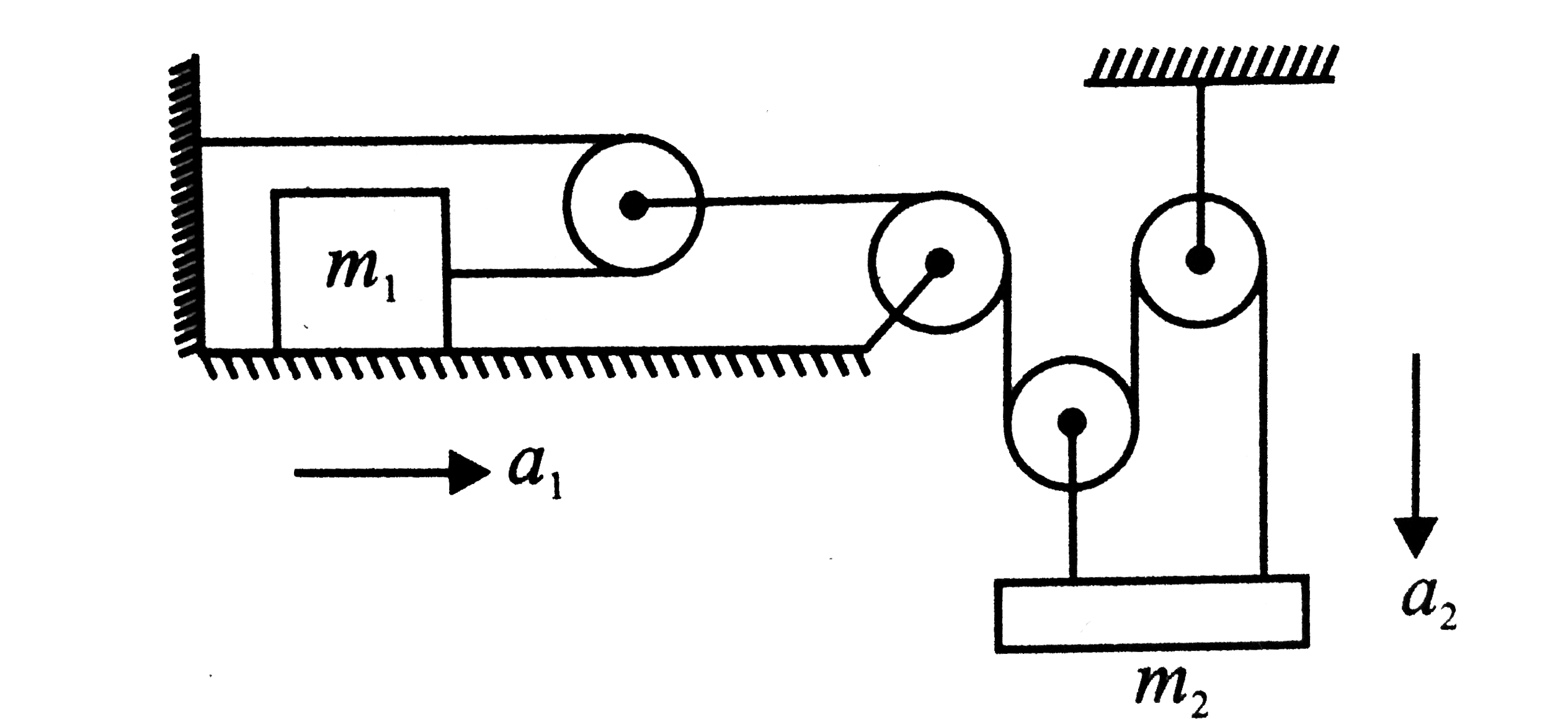
Two blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionIf a1=2 and an−an−1=2n(n≥2), find the value of a1+a2+a3+…+a20.
View Solution(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n, then a0+a1+a2+a3−a4+…a2n= .
View SolutionIf a1,a2,a3,……….are in A.P. such that a1+a5+a10+a15+a20+a24=225, then a1+a2+a3+……a23+a24 =
View SolutionIf a1anda2 are two non- collinear unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIn fig the blocks A,B,and C of mass m each have acceleration a1,a2,anda3, repectively. F1andF2 are external force of magnitude 2mgandmg, respectively. Then

View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIt a1,a2,a3a4 be in G.P. then prove that (a2−a3)2+(a3−a1)2+(a4−a2)2=(a1−a4)2
View SolutionIf a0,a1,a2,… are the coefficients in the expansion of
(1+x+x2)n in ascending powers of x, prove that
a0a2−a1a3+a2a4−…+a2n−2a2n=an+1 .
View SolutionA1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View Solution
