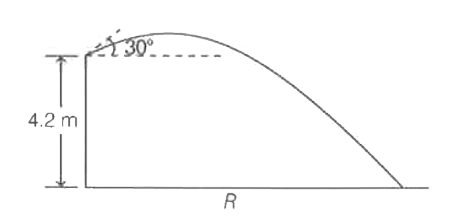
An archer shoots an arrow from a height 4.2 m above the ground with a speed 40 m/s and at angle 30∘ as shown in the figure. Determine the horizontal distance R covered by the arrow, when it hits the ground, (Take g=10m/s2)
 Solution in Telugu
Solution in Telugu
185√3m
84√3m
68√3m
95√3m
The correct Answer is:B
Given, speed of arrow,
v=40m/sandθ=30∘

Horizontal range R1 covered by the arrow is given by
R1=v2sin2θg
=402sin(2×30)10=160×sin60∘
=160√32=80√3m
If t be the time taken by the arrow reaching from B to C, then from the second equation of motion,
⇒h=ut+12gt2
here, h=4.2m, u=vsin30∘
4.2=vsin30∘t+12gt2
4.2=40×120t+12×10t2
4.2=20t+5t2
50t2+200t−42=0
25t2+100t−21=0
Solving the quadratic equation, t=15s
Distance travelled in horizontal direction is given by
R2=vcos30∘×t
=40√32×15=4√3m
Hence, the horizontal distance covered by the arrow R=R1+R2
=80√3+4√3)=84√3m
Topper's Solved these Questions
Similar Questions
Identify the correct option.
View SolutionA body is projected horizontally from a height of 20 m . It reaches the ground at a horizontally distance of 40 m . The speed of practicle when it hits the ground is
View SolutionA ball is rolled off the edge of a horizontally table at as speed of 4 m//s . It hits the ground after 0.8 s . (i) it hits the ground at a horizontal distance 3.2 m from the edge of the table (ii) The speed with which it hits the ground is 4sqrt(5) m//s (iii) Height of the table is 3.2 m (iv) it hits the ground at an angle of tan^(-1)(2) to the horizontally
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA balloon is going up with a uniform speed 20 m/s. It was at a height of 100 m from ground, when a stone is dropped from its basket. Find the time taken by the stone to reach the groimd and the height of the balloon from the ground, when stone hits the ground. (Take g = 10 m//s^(2) )
View SolutionThe initital speed of an arrow shot from s bow, at an elevation of 30^(@) , is 15 m s^(-1) , Find the velocity when it hits the ground back.
View SolutionSuppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of 60∘. What is the distance between you and the object ?
View SolutionAn arrow is launched upward with an initial speed of 70m/s ( meters per second). The equation v2=v20−2gh describes the motion of the arrow, where v0 is the initial speed of the arrow, v is the speed of the arrow as it is moving up in the air, h is the height of the arrow above the ground, t is the time elapsed since the arrow was projected upward, and g is the acceleration due to gravity ( approximately 9.8m/s2). What is the maximum height from the ground the arrow will rise to the nearest meter?
View SolutionA particle is relased from a height 20 m from the ground . After how much time and with what speed the particle hits time and with what speed the particle hits the ground ?
[Take :g=10m⋅s−2]
View SolutionAn arrow is shot horizontally from a height of 4.9 m above the ground. The initial speed of the arrow is 45 m/s. Neglecting friction, how long will it take the arrow to hit the ground?
View SolutionSuppose you are shooting an arrow from the top of a building at an height of 6 m to a target on the ground at an angle of depression of 60∘. What is the distance between you and the object?
View SolutionSuppose you are shooting an arrow from the top of a building at an height of 6 m to a target on the ground at an angle of depression of 60∘. What is the distance between you and the object?
View SolutionSuppose you are shooting an arrow from the top of a building at an height of 6 m to a target on the ground at an angle of depression of 60∘. What is the distance between you and the object?
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2].
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2].
View Solution