Consider a toroid with rectangular cross section, of inner radius a, outer radius be and height h, carrying n number of turns. Then the self-inductance of the toroidal coil when current I passing through the toroid is
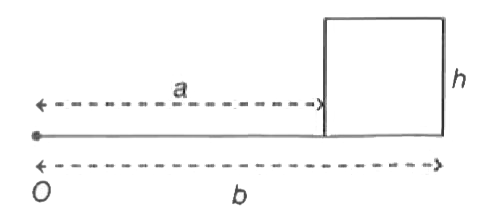
μ0n2h2πIn(ba)
μ0nh2πIn(ba)
μ0n2h2πIn(ab)
μ0nh2πIn(ab)
The correct Answer is:A
Given a toroid with a rectangular cross-section of inner readius a and outer radius b. Height of the solenoid =h
Magnetic field inside a rectangular toroid is given by
B=μ0nI2πr ......(i)
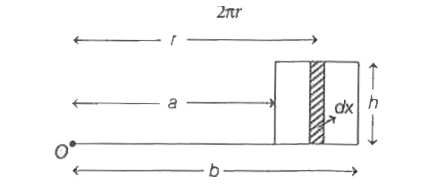
usind the infinitesimal cross-sectinoal area element.
dx=hdr
∴ Flux passing through the cross-section of toroid.
ϕ=∫B.dx=∫baμ0nI2πr.(hdr)
ϕ=μ0nIh2π∫ba1rdr
⇒ϕ=μ0nhI2π[logr]ba
⇒ϕ=μ0nhI2π(logb−loga)
ϕ=μ0nhI2πIn(ba)
Now, self inductance of rectangular toroid,
L=nϕI
Putting the value of ϕ we get
L=μ2nh2πIn(ba)
Topper's Solved these Questions
Similar Questions
Consider a toroid of circular cross - section of radius b, major radius R much greater than minor radius b, (see diagram) find the total energy stored in magnetic field of toroid -
View SolutionDetermine the mutual inductance of a toroid and an infinite straight wire located along the central axis of the toroid. The toroid has a rectangular cross section with inner and outer radii a and b respectively. The width of the rectangular cross section parallel to the straight wire is h. Total turns in the toroid is N.
View Solution
Knowledge Check
Consider a torod , having a circular cross-section of radius b, major radius R ( R > > b), having N turns and carrying current I. Find the total energy stored in the toroid.
Aμ0N2I2b22RBμ0N2I2b23RCμ0N2I2b26RDμ0N2I2b24RConsider a toroid of circular cross - section of radius b, major radius R much greater than minor radius b, (see diagram) find the total energy stored in magnetic field of toroid -
 AB2π2b2R2μ0BB2π2b2R4μ0CB2π2b2R8μ0DB2π2b2Rμ0
AB2π2b2R2μ0BB2π2b2R4μ0CB2π2b2R8μ0DB2π2b2Rμ0A rectangular toroid has 1000 turns. The ratio of the outer to inner diameter is 1.6 and its height is 5.0 cm. Find the flux through this toroid, if current passing through it is 1.7 A.
A8μWbB6μWbC8WbD6Wb
A toroid of 1000 turns has an average radius of 10 cm and area of cross section 15cm2. Calculate the self-inductance of the toroid.
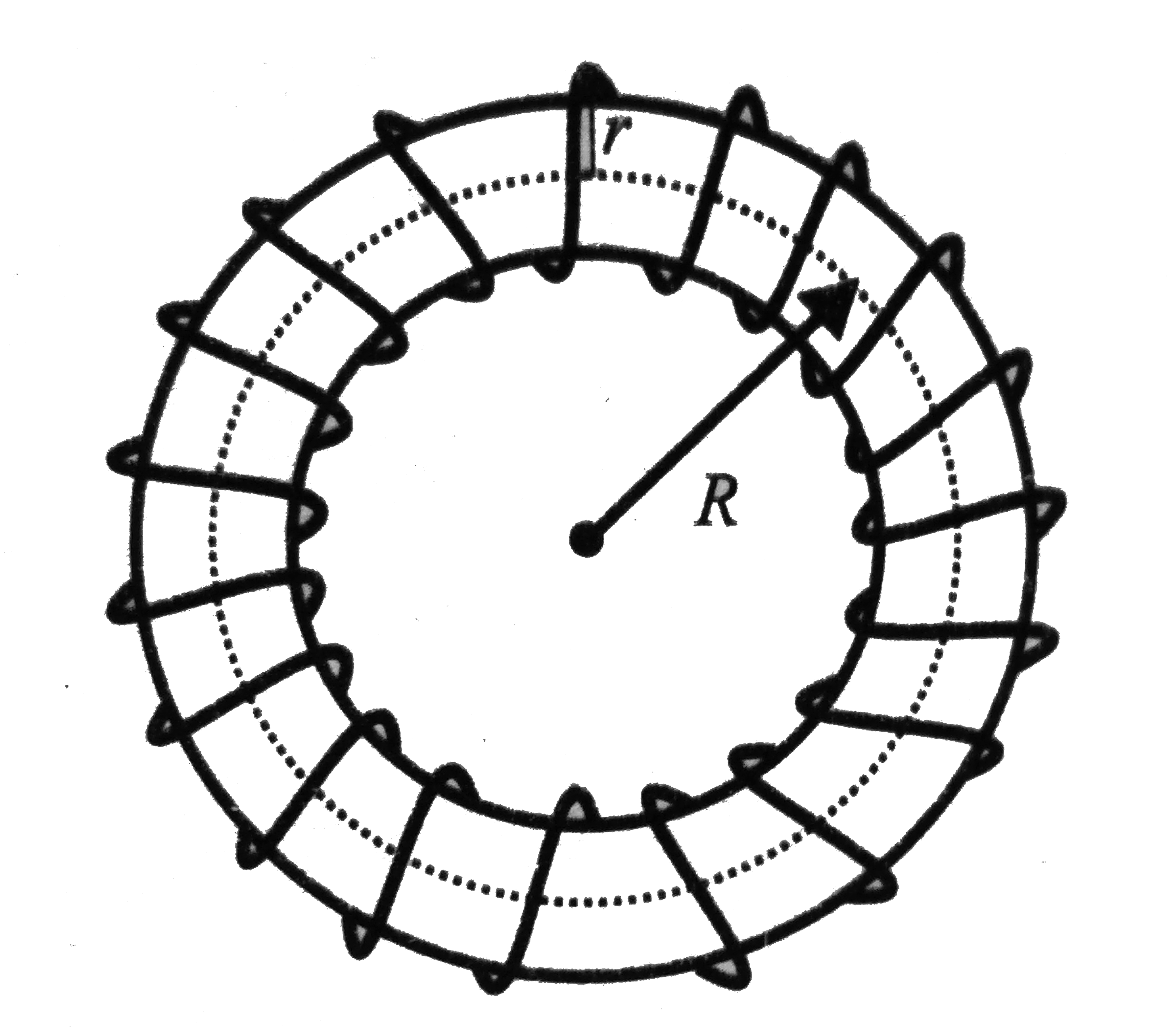
View SolutionA toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The coefficient of self-inductance of the toroid is given by
View SolutionA toroidal solenoid with an air core has an average radius of 15 cm, area of cross-section 12cm2 and 1200 turns. Obtain the self inductance of the toroid. Ignore field variations across the cross-section of the toroid.
(b) A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05 s, obtain the induced e.m.f. in the second coil.
View SolutionA toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The coefficient of self-inductance of the toroid is given by

View SolutionA toroid of core of inner radius 0.25 m and outer radius 0.26 m around which 3500 turns of a wire are wound. If the current in the wire is 11 A, then magnetic field inside the core of the toroid is
View Solution
