In the isosceles ΔABC, AB = AC , O is any point on the side BC. OP and OQ are the perpendicular distance of the sides AB and AC from O respectively. BD is the perpendicular distance of AC from B. Show that OP + OQ = BD.Solution in Bengali
Step by step video & image solution for In the isosceles DeltaABC, AB = AC , O is any point on the side BC. OP and OQ are the perpendicular distance of the sides AB and AC from O respectively. BD is the perpendicular distance of AC from B. Show that OP + OQ = BD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEOREMS ON AREASBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON AREASEXERCISE - EXERCISE-3
40 Videos
- SET THEORYBOOK - CALCUTTA BOOK HOUSECHAPTER - SET THEORYEXERCISE - EXERCISE-1
37 Videos
- THEOREMS ON CONCURRENCEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON CONCURRENCEEXERCISE - EXERCISE Long-answer type questions
17 Videos
Similar Questions
D is any point on the side QR of the parallelogram PQRS. ΔPQDandΔSDR have the areas 16 sq.cm and 20 sq.cm respectively, then QD : RD =
View SolutionState which of the following are sets and which are not:
A=A group of students of class-IX having heights from 4ft to 5ft,
View SolutionFind the value of k for which the given value is a solution of the given equation 7x2+kx−3=0 at x=23
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View Solutionआकृति 6 .21 में क्रमशः OP,OQ और OR पर स्थित बिंदु A,B और C इस प्रकार है कि AB||PQ और AC||PR है दर्शाइए कि BC||QR है
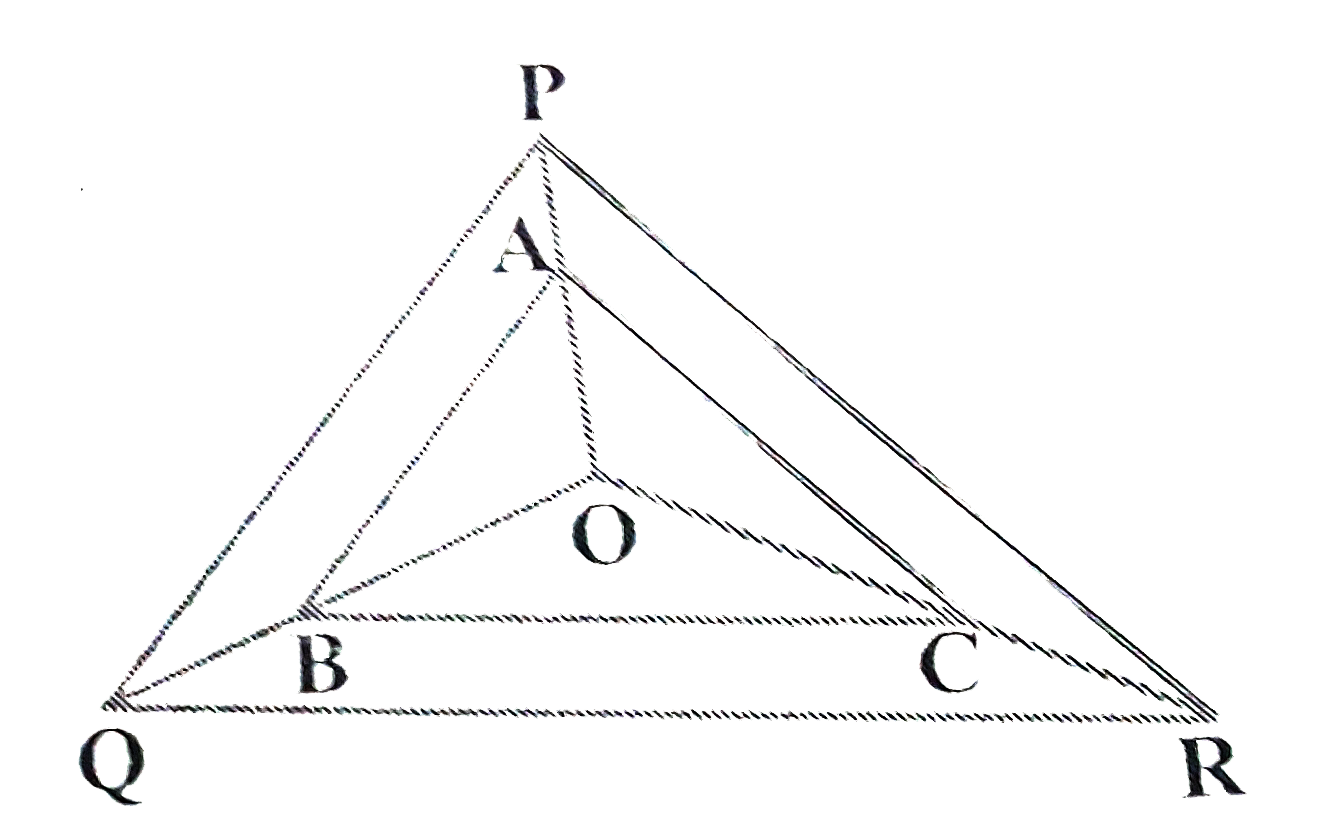
View Solutionएक समद्विभाहु त्रिभुज ABC में भुजा AB = भुजा AC तथा बिंदु B से भुजा AC पर BD लम्ब है । सिद्ध कीजिए कि BC2=2AC.DC.
View Solutionनिम्न आकृति में क्रमशः OP , OQ और OR पर स्थित बिन्दु A , B और C इस प्रकार हैं कि AB∣∣PQ और AC∣∣PR हैं । दर्शाइए कि BC∣∣QR हैं |

View Solutionसंलग्न चित्र में OP,OQ और OR पर क्रमशः बिंदु A,B और C इस प्रकार है कि AB||PQ और BC||QR है दिखाइए कि AC||PR
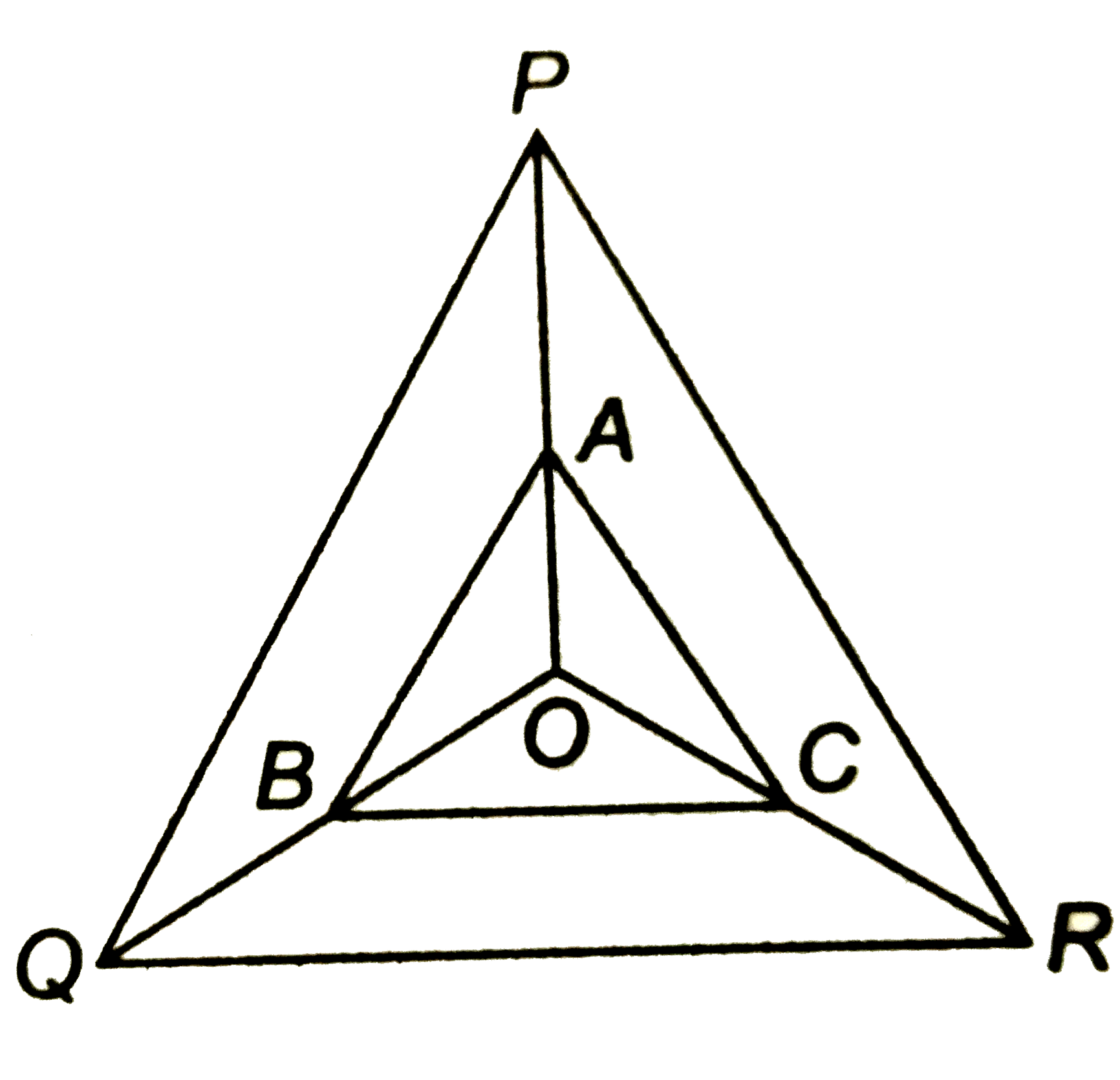
View SolutionIn Fig A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR . Show that BC || QR.
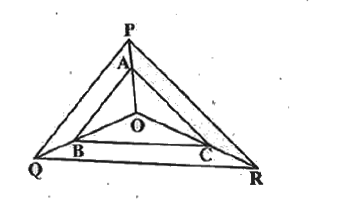
View SolutionThe diagonals AC and BD of the parallelogram ABCD intersect each other at O . Any straight line passing through O intesects the sides AB and CD at the points P and Q respectively . Prove that OP = OQ.
View SolutionOn the outside of the equilateral triangle ABC and in the angular region ∠ABC, O is a point. OP, OQ and OR are the perpendiculars drawn from O to the sides. AB, BC and CA respectively. Prove that the height of the triangle = OP + OQ - OR.
View SolutionIn the adjacent figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC||PR. Show that BC || QR.
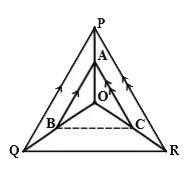
View SolutionIn the adjacent figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC||PR. Show that BC || QR.
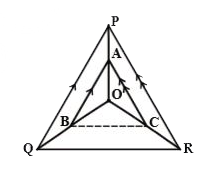
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

View SolutionIn the given figure, A, B and C are points on OP, OQ and OR respectively such that AB||PQ and AC||PR. Show that BC∣∣QR.
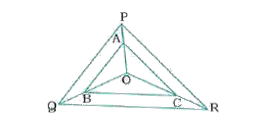
View Solution
