P is any point in the interior of the parallelogram ABCD. Prove that ΔAPD+ΔBPC = 12 parallelogram ABCD.Solution in Bengali
Step by step video & image solution for P is any point in the interior of the parallelogram ABCD. Prove that DeltaAPD+DeltaBPC = 1/2 parallelogram ABCD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEOREMS ON AREASBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON AREASEXERCISE - EXERCISE-3
40 Videos
- SET THEORYBOOK - CALCUTTA BOOK HOUSECHAPTER - SET THEORYEXERCISE - EXERCISE-1
37 Videos
- THEOREMS ON CONCURRENCEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON CONCURRENCEEXERCISE - EXERCISE Long-answer type questions
17 Videos
Similar Questions
D is any point on the side QR of the parallelogram PQRS. ΔPQDandΔSDR have the areas 16 sq.cm and 20 sq.cm respectively, then QD : RD =
View SolutionState which of the following are sets and which are not:
A=A group of students of class-IX having heights from 4ft to 5ft,
View SolutionFind the value of k for which the given value is a solution of the given equation 7x2+kx−3=0 at x=23
View SolutionIf P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the are of parallelogram.
View SolutionABCD एक समांतर चतुर्भुज है तथा P इसका कोई अंतः बिंदु है सिद्ध कीजिए कि ΔABP का क्षेत्रफल +ΔDCP का क्षेत्रफल =12 समांतर चतुर्भुज ABCD का क्षेत्रफल
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ΔAPD=ΔCPD.
View SolutionIn the figure ''P'' is a point in the interior of a parallelogram ABCD.
Show that area of ΔAPD+ area of ΔPBC = area of ΔAPB+ area of ΔPCD.
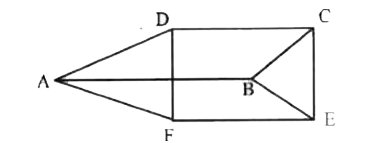
View Solutionचित्र में ABCD और AFEB समान्तर चतुर्भुज हैं। सिद्ध कीजिए कि CDFE समान्तर चतुर्भुज हैं।
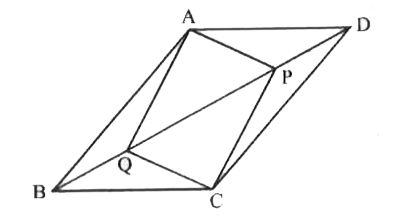
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु Pऔर Q इस प्रकार स्थित हैं कि DP = BQ हैं ( देखिए आकृति)।दर्शाइए कि-
ΔAPDE≅ΔCQB
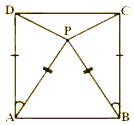
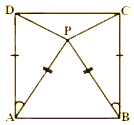
View SolutionIn the adjacent figure ABCD is a square and Delta APB is an equilateral triangle. Prove that DeltaAPD ~= DeltaBPC .
View SolutionIn the adjacent figure ABCD is a square and ΔAPB is an equilateral triangle. Prove thatΔAPD≅ΔBPC.
View SolutionIn the adjacent figure ABCD is a square and ΔAPB is an equilateral triangle. Prove thatΔAPD≅ΔBPC.
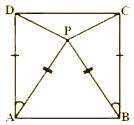
View SolutionIn the adjacent figure ABCD is a square and ΔAPB is an equilateral triangle. Prove thatΔAPD≅ΔBPC.
View SolutionABCD is a parallelogram. P is any point on AD, such that AP=13AD and Q is a point on BC such that CQ=13BC . Prove that AQCP is a parallelogram.
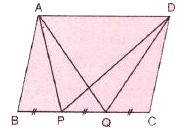
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View Solution
