An iron rod of length 1.5m lying on a horizontal table is pulled up from one end along a vertical line so as to move it with a constant velocity 3m/s, while the other end of the rod slides along the floor. After how much time the speed of the end sliding on the floor equals to the speed of the end being pulled up.
12√2s
1√2s
3√2s
14s
The correct Answer is:A
Length of an iron rod, l=1.5m
Constant velocity,V=3m/s
The diagram for given situation is given by

Since, velocity is constant, velocity of end P at point R is also 3m/s
After time 't', position of RS of rod is,
(l−x)2+(3t)2+=l2
(1.5−x)2+9t2=(1.5)2
(1.5)2+x2−2(1.5)(x)+9t2=2.25
2.25+x2−3x+9t2=2.25
x2−3x+9t2=0 ...(1)
Equation of motion of rod moving with constant velocity is,
x=ut+12at2
x=ut+0
x=3t ...(2)
Substituting equation (2) in equation (1),
(3t)2−3(3t)+9t2=0
9t2−9t+9t2=0
18t2−9t=0
2t−1=0
2t−1=0
∴t=12
Topper's Solved these Questions
Similar Questions
A meter stick AB is lying on a horizontal table. Its end A is pulled up so as to move it with a constant velocity VA=4ms–1 along a vertical line. End B slides along the floor.

(a) After how much time (t0) speed (VB) of end B becomes equal to the speed (VA) of end A ?
(b) Find distance travelled by the end B in time t0.
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View Solution
Knowledge Check
A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
AmglBmgl/2Cmgl4D2mglA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L
A rod of length 2 m is held vertically with one of its end on the floor. It is then allowed to fall. Calculate the speed of the other end when it strikes the floor. Assume that the end of the rod which is on the floor does not slip.
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collision
View Solution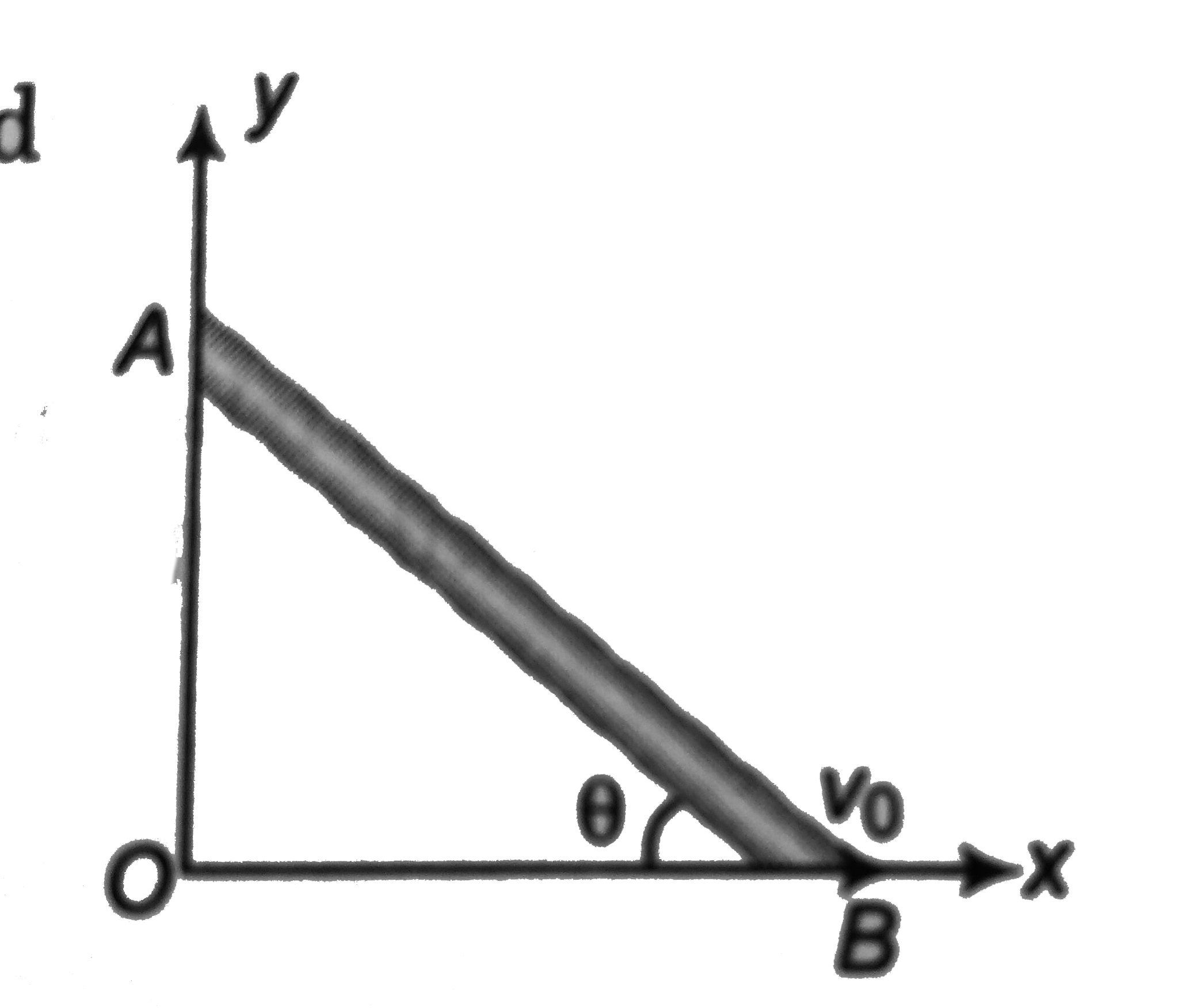
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
View Solution
