ABCD is a parallelogram and P is the mid point of the side AD. The line BP meets the diagonal AC in Q. Then the ratio =.
The correct Answer is:A
Topper's Solved these Questions
- EAMCET -2016 (TS)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (TS)EXERCISE - PHYSICS
33 Videos
- EAMCET -2016 (TS)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (TS)EXERCISE - CHEMISTRY
36 Videos
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
- EAMCET QUESTION PAPER 2017BOOK - SIA PUBLICATIONCHAPTER - EAMCET QUESTION PAPER 2017EXERCISE - CHEMISTRY
6 Videos
Similar Questions
□ABCD is a parallelogram. P is the midpoint of side CD. Seg BP meets diagonal AC at X. Prove that 3AX=2AC.
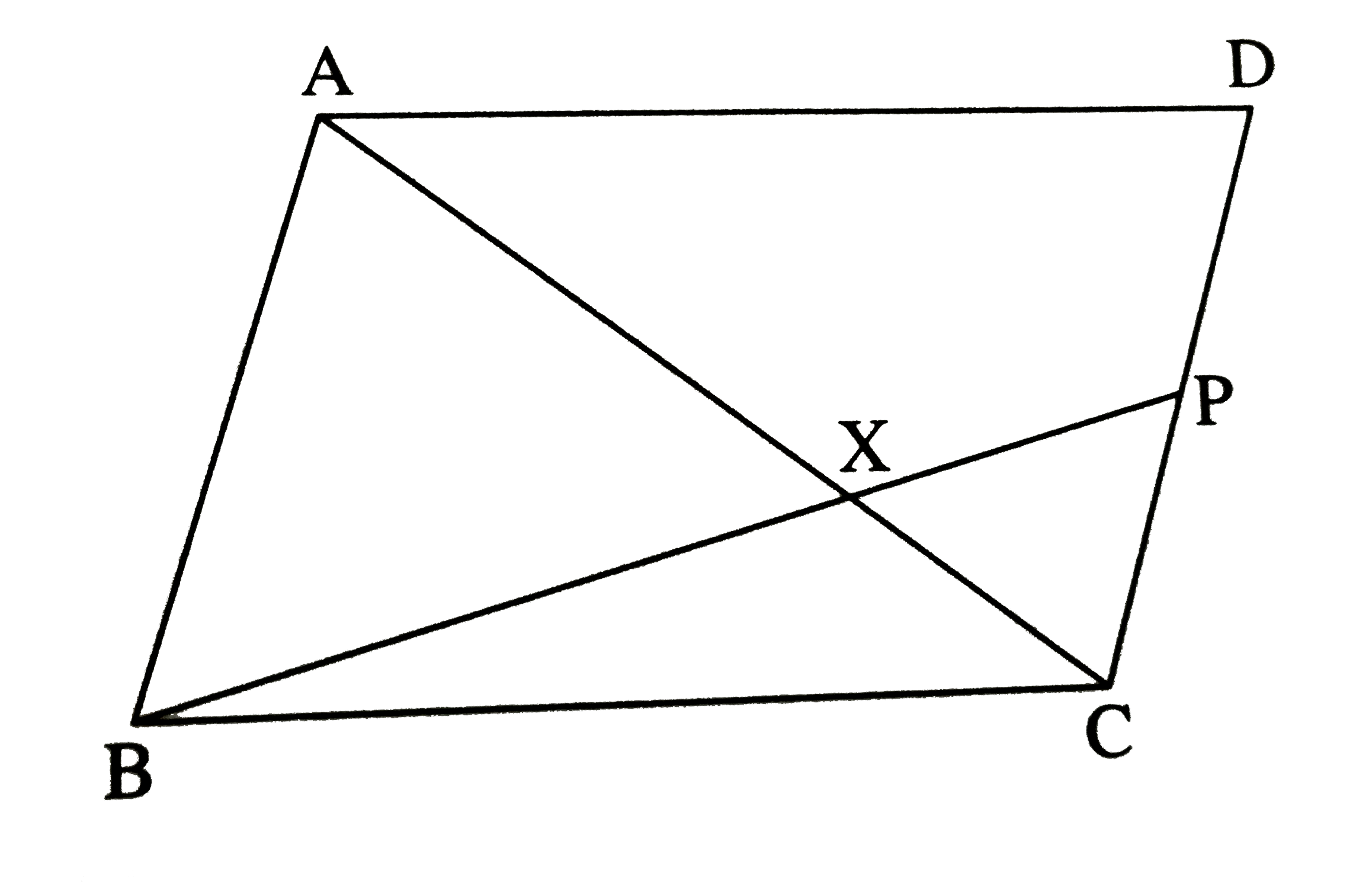
View SolutionABCD is a parallelogram and P is a point on the segment ¯¯¯¯¯¯AD dividing it internally in the ratio 3:1 the line ¯¯¯¯¯¯BP meet the diagonal AC in Q. Then the ratio AQ:QC is
View Solution
Knowledge Check
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by ACABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of theseABCD is a parallelogram and O is the point of intersection of its diagonals. If points P, Q, R, S are the mid-points of OA, PB, QC, RD respectively, then the points Q, O, S
Aforms a triangleBare non-coplanarCare collinearDare non-collinear
P is the mid-point of the side AD of the parallelo- gram ABCD. The line BP meets the diagonal AC in Q and the line CD in R. Then RQ:QB is equal to
View SolutionShow that the line joining any vertex of a parallelogram to the mid - point of an opposite side divides the opposite diagonal in the ratio 2 : 1.
View SolutionABCD is a parallelogram. E; F are mid point of BC; CD respectively. AE; AF meet the diagonal BD at points Q and P respectively. Show that points P and Q trisect DB.
View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionABCD is a parallelogram, P and Q are the points on the diagonal AC such that AP=QC, then quadrilateral BPDQ is a :
View Solution
