ABCD is a parallelogram, P and Q are the points on the diagonal AC such that AP=QC, then quadrilateral BPDQ is a :
trapezium
parallelogram
square
none of these
The correct Answer is:B
To solve the problem, we need to analyze the properties of the parallelogram ABCD and the points P and Q on the diagonal AC.
1. Identify the Parallelogram:
- We have a parallelogram ABCD. In a parallelogram, opposite sides are equal and parallel.
- Let’s denote the vertices as follows: A (top left), B (top right), C (bottom right), D (bottom left).
2. Draw the Diagonal AC:
- Draw the diagonal AC. This diagonal divides the parallelogram into two triangles: ΔABC and ΔADC.
3. Locate Points P and Q:
- Points P and Q are located on diagonal AC such that the lengths AP and QC are equal.
- This means that if we let AP = x, then QC = x as well.
4. Determine the Lengths:
- Since AP = QC, we can denote the length of AC as the total length (let’s say it is L).
- Therefore, we have:
- AC = AP + PQ + QC
- L = x + PQ + x
- L = 2x + PQ
- From this, we can express PQ as:
- PQ = L - 2x.
5. Connect Points B, P, D, and Q:
- Now, we will connect points B to P and D to Q to form the quadrilateral BPDQ.
- We also connect B to D to complete the quadrilateral.
6. Analyze Quadrilateral BPDQ:
- We need to determine the properties of quadrilateral BPDQ.
- Since AP = QC, the segments BP and DQ will also be equal in length due to the properties of the parallelogram (opposite sides are equal).
7. Check for Parallelism:
- Since AB is parallel to CD (properties of parallelogram) and BP is equal to DQ, we can conclude that:
- BP || DQ (because they are both segments connecting points on the same diagonal).
- Therefore, we have two pairs of opposite sides that are equal and parallel.
8. Conclusion:
- Since both pairs of opposite sides are equal and parallel, quadrilateral BPDQ is a parallelogram.
Final Answer:
Quadrilateral BPDQ is a parallelogram.
---
- We have a parallelogram ABCD. In a parallelogram, opposite sides are equal and parallel.
- Let’s denote the vertices as follows: A (top left), B (top right), C (bottom right), D (bottom left).
- Draw the diagonal AC. This diagonal divides the parallelogram into two triangles: ΔABC and ΔADC.
- Points P and Q are located on diagonal AC such that the lengths AP and QC are equal.
- This means that if we let AP = x, then QC = x as well.
- Since AP = QC, we can denote the length of AC as the total length (let’s say it is L).
- Therefore, we have:
- AC = AP + PQ + QC
- L = x + PQ + x
- L = 2x + PQ
- From this, we can express PQ as:
- PQ = L - 2x.
- Now, we will connect points B to P and D to Q to form the quadrilateral BPDQ.
- We also connect B to D to complete the quadrilateral.
- We need to determine the properties of quadrilateral BPDQ.
- Since AP = QC, the segments BP and DQ will also be equal in length due to the properties of the parallelogram (opposite sides are equal).
- Since AB is parallel to CD (properties of parallelogram) and BP is equal to DQ, we can conclude that:
- BP || DQ (because they are both segments connecting points on the same diagonal).
- Therefore, we have two pairs of opposite sides that are equal and parallel.
- Since both pairs of opposite sides are equal and parallel, quadrilateral BPDQ is a parallelogram.
Quadrilateral BPDQ is a parallelogram.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.560videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2100videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
ABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
View SolutionABCD is a quadrilateral and BD is one of its diagonals, as shown in the figure. Prove that quadrilateral ABCD is a parallelogram, also find its area.
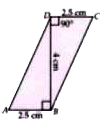 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of these - Question 2 - Select One
ABCD is a parallelogram. If P be a point on CD such that AP=AD , then the measure of ∠PAB+∠BCD is:
A180∘B225∘C240∘D135∘ - Question 3 - Select One
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NM
ABCD is a / gram. P and Q are two points on AB and CD such that AP : PB = 2:3 , DQ = QC = 4 : 1 Find the ratio of area of Δ DPQ and '// ABCD
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.
 View Solution
View SolutionLet ABCD is a parallelogram and →AC,→BD be its diagonal, then →AC+→BD is
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
View Solution

