दो सर्वसम बिलियर्ड गेंदें किसी दृढ़ दीवार से समान चाल से , परंतु भिन्न कोनों पर टकराती है तथा नीचे दर्शाए चित्र की भाँति चाल में बिना क्षय हुए परावर्तित हो जाती है ।
(i) प्रत्येक गेंद के कारण दीवार पर बल की दिशा क्या है ? तथा (ii) दीवार द्वारा दोनों गेंदों पर लगे आवेगों का अनुपात क्या है ?
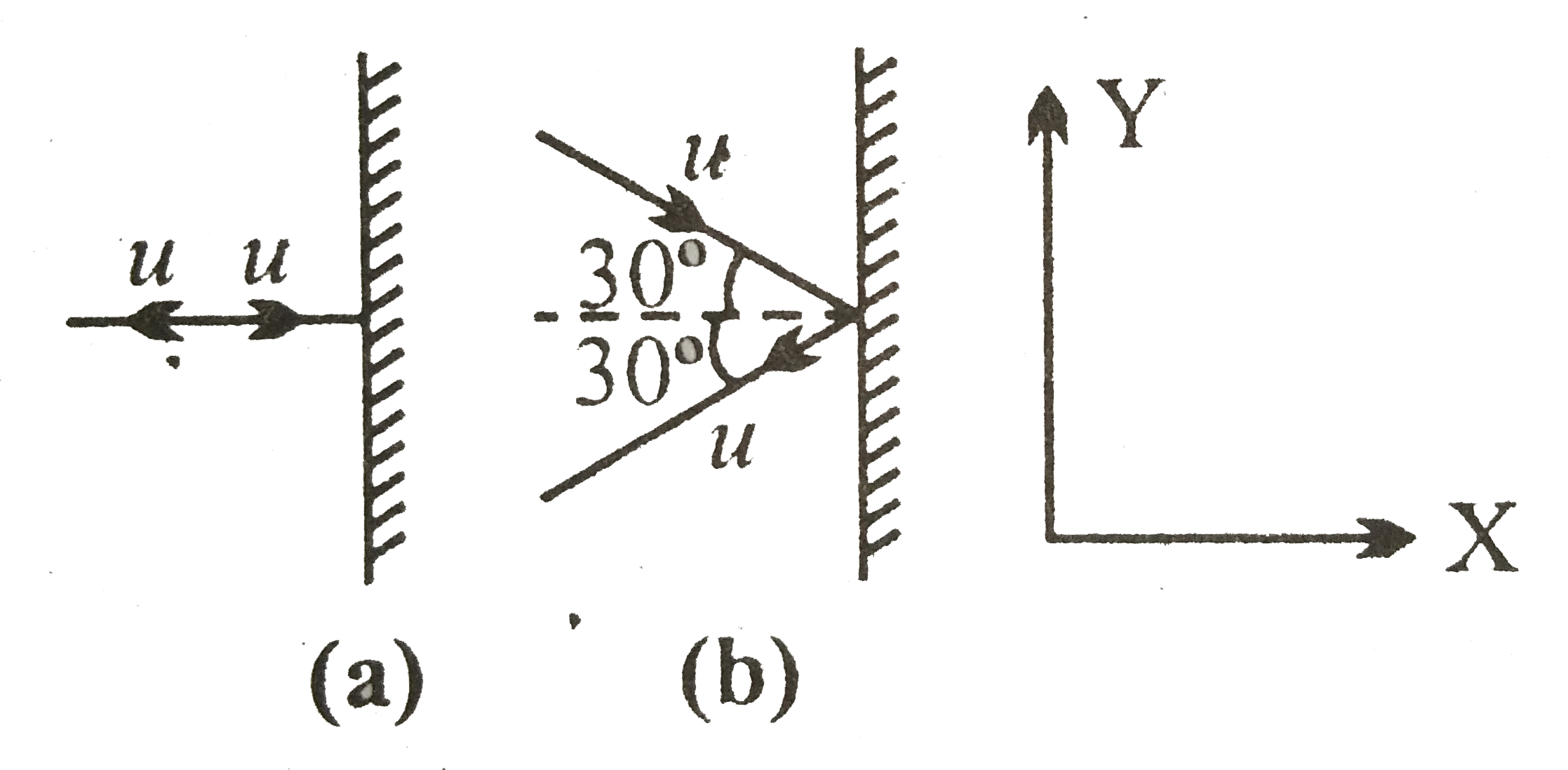
माना प्रत्येक गेंद का द्रव्यमान m है|
(i ) (a ) पहले गेंद के वेग के संवेग को X - अक्ष और Y - अक्ष के अनुदिश वियोजित करने पर, टकराने के पूर्व
संवेग
तथा
टकराने के पश्चात संवेग
तथा
अतः X - अक्ष के अनुदिश संवेग में परिवर्तन
Y - अक्ष के अनुदिश संवेग में परिवर्तन = 0
आवेग संवेग में परिवर्तन के बराबर होता है|
X - अक्ष के अनुदिश आवेग
Y - अक्ष के अनुदिश आवेश = 0
आवेग सदिश और बल की दिशा समान होती है । अतः गेंद पर दीवार द्वारा लगाया गया बल ऋणात्मक X - अक्ष के अनुदिश होगा । न्यूटन के गति के तृतीय नियमानुसार गेंद द्वारा दीवार पर लगाए गए बल की दिशा धनात्मक X - अक्ष के अनुदिश होगी ।
(b) दूसरी गेंद के संवेग को X - अक्ष एवं Y - अक्ष के अनुदिश वियोजित करने पर
टकराने के पूर्व
टकराने के पश्चात
इस प्रकार X - अक्ष के अनुदिश संवेग में परिवर्तन
तथा Y - अक्ष के अनुदिश संवेग में परिवर्तन
आवेग संवेग में परिवर्तन के बराबर होता है ,
X - अक्ष के अनुदिश आवेश
Y - अक्ष के अनुदिश आवेग = 0
आवेग तथा बल की दिशा समान होती है । अतः दीवार के कारण गेंद पर लगाने वाला बल ऋणात्मक X - अक्ष के अनुदिश होगा । न्यूटन के गति के तृतीय नियम के अनुसार गेंद द्वारा दीवार पर लगाये गये बल की दिशा धनात्मक X - अक्ष के अनुदिश होगी ।
( ii ) दीवार द्वारा दोनों गेंदों पर लगे आवेगों का अनुपात
Topper's Solved these Questions
- गति के नियम BOOK - NAVBODHCHAPTER - गति के नियम EXERCISE - बोधात्मक प्रश्न
8 Videos
- गति के नियम BOOK - NAVBODHCHAPTER - गति के नियम EXERCISE - तथ्यात्मक प्रश्न
13 Videos
- गति के नियम BOOK - NAVBODHCHAPTER - गति के नियम EXERCISE - आंकिक उदाहरण
34 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
51 Videos
- गतिमान आवेश और चुम्बकत्व BOOK - NAVBODHCHAPTER - गतिमान आवेश और चुम्बकत्व EXERCISE - पाठ्यपुस्तक के प्रशोत्तर
46 Videos
Similar Questions
क्या प्रकृति में ''एकल विलगित बल'' का अस्तित्व है?
View Solutionएक घोड़ा शून्य आकाश में न तो गाड़ी खींच सकता है और न ही दौड़ सकता है , क्यों ?
View Solution5 किग्रा द्रव्यमान की एक ट्रॉली पर एक बल लगाने पर उसमें 10 मीटर/सेकंड2 का त्वरण उत्पन्न हो जाता है । आरोपित बल की गणना कीजिए ।
View Solutionकिसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिह्व समझना महत्वपूर्ण है । सावधानीपूर्वक बताइए कि निम्न लिखित राशियाँ धनात्मक हैं या ऋणात्मक-
( a ) किसी व्यक्ति द्वारा किसी कुँए में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य ।
View Solutionतार की एक वृत्ताकार कुंडली में 100 फेरे हैं, प्रत्येक की त्रिज्या 8.0cm है और इनमे से 0.40A विघुत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
View Solutionक्या दो संख्याओं का म.स. (H.C.F.) तथा ल.स. (L.C.M)समान हो सकता है ? कारण दीजिये।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionएक थैले में 10 गेंदे है जिनमे से प्रत्येक पर से तक के अंको में से अंक लिखा है। यदि थैले से 4 गेंदे उत्तरोत्तर पुनः वापस रखते हुए निकाली जाती है , तो इसी क्या प्रायिकता है कि उनमे से किसी गेंद अंक 0 नहीं लिखा हो ?
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionजॉर्ज पंचम की नाक' पाठ के माध्यम से लेखक ने समाज पर क्या व्यंग्य किया है?
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View SolutionIf a boat goes upstream at a speed fo 18 km /hr and comes back the same distance at 30 km/ hr.What is the average speed (in km /hr)for the total journey?
कोई नाव धारा के विपरीत दिशा में 10 किलोमीटर /घंटा की चाल से चलती है और समान दूरी पर 30 किलोमीटर/घंटा की चाल से वापस आती है। कुल यात्रा के लिए औसत चाल किलोमीटर/ घंटा में) क्या है?
View SolutionA ladder is placed against a wall such that it just reaches the top of the wall.The foot of the ladder is at a distance of 5 metres from the wall. The angle of elevation of the top of the wall from the base of the ladder is 15^@ . What is the length (in metres) of the ladder? एक सीढ़ी दीवार के सहारे इस प्रकार खड़ी है कि वह दीवार की चोटी तक पहुँचाती है। सीढ़ी का आधार दीवार से 5 मीटर की दूरी पर है। सीढ़ी के आधार से दीवार की चोटी का उन्नयन कोण 15^@ है। सीढ़ी को लंबाई (मीटर में) क्या है?
View Solutionजो चीजों से उठती अंधेपन की भाप पर दुलक जाती है' में कौन-सा अलंकार है ?
View Solution
